So this virus outbreak thing is interesting isn't it?
As a mathematician-in-training, what I'm finding more interesting is the lack of good statistics on what's happening. The UK government were initially publishing new infections within England and in the whole of the UK. In addition, they were publishing the total UK infected, and total UK deaths. They stopped reporting anything on March 5th.
Though as well as keeping track of government announcements, I've also been keeping record of daily updates that the World Health Organisation (WHO) have been making.
Here's a link to their European map.
Here's a link to their global map.
On a daily basis, I've been recording UK totals from their site. You can see them graphed below:
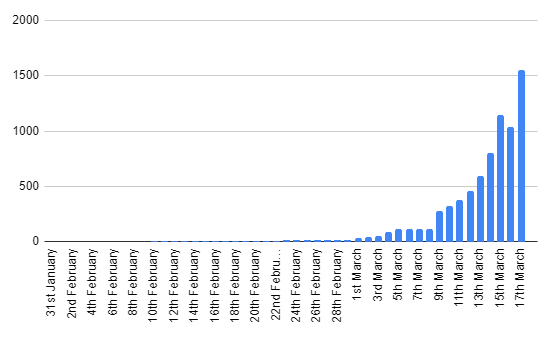
You can't see it, but the values for the first 9 days are just two people.
Though see how there's a dip on March 16th? How could there possibly be a dip in cases for one day by over 100 people? It seems even the pros can get their numbers wrong. Bad work, WHO. 🙁
Also, you'll notice from around March 5th to March 8th, it goes flat. These are days on which I didn't check the figures.
From these total cases per day, I've calculated new cases per day.
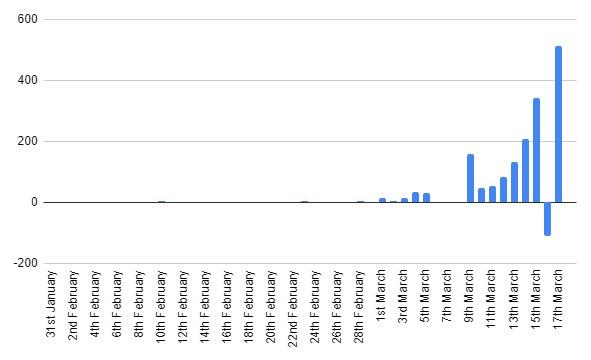
See that negative number of new cases on March 16th? Insert eyeroll emoji.
There's also a spike on March 9th, this is just total new cases from March 5th to March 9th. -catching up from when I didn't check on the totals on these days.
But as you can see, as predicted, this initial growth is basically exponential. Fairly typical for an epidemic apparently.
So the big question is... what next?! -and here's where my mathematics and statistics study comes in handy... I've recently finished a section on epidemics! What better time to apply some of my learning!
First off, it's worth mentioning that all the epidemic modelling I've learned about assumes homogeneous mixing. This is the kind of mixing that occurs in a family home. ie: there's more or less an equal chance of me having contact with one person than there is anyone else. In real life this, of course, isn't true. Living in London, I'm less likely to be in contact with someone in Edinburgh than I am someone I travel with on the London Underground every day. Also important point: homogeneous mixing means no quarantining. So all of the below is essentially average worst-case.
So with the proviso that these results will probably (more than likely) be wildly inaccurate, let's get started! We need a few important numbers, some of which we've already got:
- We need the starting number of infected (y0), in this case 2.
- We need the starting number of non-infected (x0), that's the total population of the UK minus 2. I decided to estimate the current population at 67.44 million.
- We need the epidemic number, ρ. This is calculated in the following way:
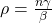
Where:
- n is the total population (67.44 mil).
- γ is the parameter in the exponential distribution that describes the mean recovery time of the virus. (It's random).
- β is the parameter in the Poisson distribution that describes the mean contact rate (per day). (Also random).
Which is fine, but how do we know what γ and β are? Well there's a number called R0 ("R-naught") that I've NOT been taught about that represents the contagiousness of a virus. Interestingly, I've found two completely opposed descriptions of this number:
- https://en.wikipedia.org/wiki/Basic_reproduction_number
- https://towardsdatascience.com/social-distancing-to-slow-the-coronavirus-768292f04296
Though we all know how reliable wikipedia is, and I've just found this Stanford paper which supports the towardsdatascience description:
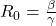
Therefore:
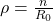
Hooray. Imperial College London seems to estimate the R0 of COVID-19 to be 2.4, so let's run with that.
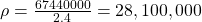
Max Number Of Infectives At One Time
Once we have all this, we can work out the maximum number of infectives at any one time. ie: the peak of the infection in the population, ymax:
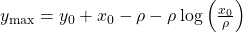
Now we can plug all the numbers in to find ymax! So:
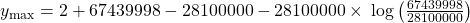
Hence:
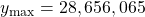
Which is 42.5% of the population infected at one time! Ouch! At least you'll know that if we (in our theoretical UK) hit 28 million with no quarantining, we'd be at the peak of the outbreak.
Other sources state that COVID-19 actually has a range of R0 values, 1.4-3.8-ish, so the band of possible outcomes without quarantining is actually quite broad. But from this it's possible to work out a best-case/worse-case comparison:
An R0 of 1.4 would mean a max of 12.2 million (18% of the population), and an R0 of 3.8 would mean a max of 39.4 million (58% of the population) at one time.
Number Of People Not Affected
The following assumes that the whole debacle is over. Everyone that has caught the virus from it has now recovered. How many people were not affected?
This is found using the following iteration formula:
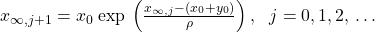
Initially x_{inf,j} is zero, and you use your result x_{inf,j+1} to calculate x_{inf,j+2}, and so on. This eventually settles down to the number of people not affected!
So using the power of spreadsheets, and not taking up the space here with columns and columns of numbers:
- R0 of 1.4 would mean 32.98 million people are not affected.
- R0 of 2.4 would mean 8.29 million people are not affected.
- R0 of 3.8 would mean 1.66 million people are not affected.
You can imagine that an increase in quarantining means a lower R0. Seems that could have a big effect.
#ImNotAStatisticianButItsStillFunLookingAtNumbers



