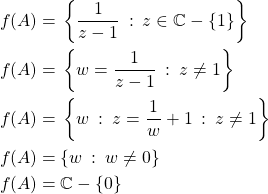Category Archives: Analysis

Analysis, Complex Analysis, Proofs, Pure Maths

Complex Analysis Assignment 1

December 29, 2020 Adrian

My first complex analysis assignment has been marked and returned. I don't think I've ever felt the urge quite so much to learn from my mistakes.

Consequently there has been quite a lot of post-assignment learning... :/

This assignment featured a very brief introduction to complex numbers as a refresher, then broadly covered complex functions, the concept of continuity and complex differentiation.

So in no particular order, below are some notes on mistakes I made and how I could've avoided them! There's a lot to reflect on here...

Read questions carefully. One of the first very simple questions read "express $z$ in polar form and determine all fourth roots". I did the second bit, but not the first.

I feel this is a bit "Complex Numbers 101", but the square root sign is defined as the principal square root (of a complex number), i.e. there's no need to calculate the second root.

If you're using the triangle inequality, state it specifically.

Again, this is fairly "Complex Numbers 101", but the polar form of a complex number isn't just a cosine function as the real part, and a sine function as the imaginary part. The arguments to both functions must be identical to qualify as "polar form". ie, you should be able to write the complex number as an exponential form.

Top tip: Be mindful about using identities. In complex analysis there are loads of them and they help a great deal.

When working out the inverse of a complex function, it's important to use your common sense. Part of one inverse I'd calculated had a square root in it. Just by looking at that, you know it could never produce a unique answer (it isn't a one-to-one function).

For another, I had to find the inverse of $\text{Log}(3z)$ and the domain of that inverse. I got this spectacularly wrong. I'd written: given $w=\text{Log}(3z)$ , hence $z=e^{3w}$ .

Trick here was to exponentiate each side, leading to $e^{w}=3z$ . But the domain of the inverse isn't affected by the "3" above, the image set of the original function is still $\{z: -\pi <\text{Im}z \leq \pi\}$ .

Some complex functions are very very different to their real equivalents. Case in point: $\text{cosh}(x)\neq 0 , \forall x \in \mathbb{R}$ , but $\exists\: z \in \mathbb{C}\: \text{s.t.}\: \text{cosh}(z)=0$ . Which leads to the next note:

If $\text{cosh}(z)$ is the divisor in a complex quotient, you need to show that it's only 0 for values outside of the given range of the equation (eg $|z|<1$ ).

For one question, I had to prove that $f(z)=z^{i},\:\: (\text{Re}\:z>0)$ was continuous. I thought this was easy.

$z^{\alpha},\: \alpha \in \mathbb{C}$ is a basic continuous function on $\mathbb{C}-\{x\in\mathbb{R} : x \leq 0\}$ . So if you let $\alpha=i$ , then $f(z)$ is continuous, right?

Not quite. I had entirely forgotten to state that the given set $(\text{Re}\:z>0)$ is a subset of the set I gave: $\mathbb{C}-\{x\in\mathbb{R} : x \leq 0\}$ .

The answer can appear obvious sometimes, but you have to keep your answer rigorous, otherwise you risk losing half marks or whole marks here and there.

Note:
$z^{\alpha} = e^{\alpha Log(z)}$
$z^{\alpha} \neq e^{z Log(\alpha)}$
🙁

For one question I had to prove whether a set was a region or not. For reference, a region is a non-empty, connected, open subset of $\mathbb{C}$ . In the usual manner, if you can prove that any of those three properties don't hold then you've managed to prove that your set isn't a region. Easy.

I realised I could prove a set was closed, and hence not a region. Turns out this was incorrect. A set being "closed" and a set being "not open" hold two completely different definitions, and are seen as different things. I was meant to show it was "not open" as opposed to showing it was "closed".

In other words, mathematically:

Closed is not the same as not-open.
Closed is not the opposite of open.
Not-open is the opposite of open.

Again, here I needed to provide a proof based on the properties of various objects. Given a set that was compact (closed and bounded), I needed to prove that a function $f$ was bounded on that set.

The Boundedness Theorem states that if a function is continuous on a compact set, then that function is bounded on that set.

The function was: $f(z) = \frac{1}{7z^{7}-1}$

I proved that the given function was continuous on it's domain, but I'd failed to prove it was continuous on the set. Here, I needed to show where the function was undefined, THEN show that those points at which it was undefined all lay outside of the set. So there was quite a lot of work I missed out from this answer.

My simultaneous requirement for the Cauchy-Riemann theorem, AND the Cauchy-Riemann Converse theorem within a proof ended up not flowing very well logically. Once again, I'd jumped ahead with my logic. As soon as I had seen something obvious, I felt the urge to state it immediately.

The Cauchy-Riemann theorem proves that a function is not differentiable at certain points. The Converse theorem then proves that a function IS differentiable on certain points. After using the Cauchy-Riemann theorem, it was extremely obvious where the function was differentiable, so I stated it. Then, as a matter of course, plodded through the Converse theorem to prove it. Complete lack of discipline! 🙂

Analysis, Complex Analysis, Proofs, Pure Maths

Complex Functions: Domains, Image Sets and Inverses

September 21, 2020 Adrian

I can imagine having to refer to these notes regularly, so I'm putting them here!

Image Sets

State the domain $A$ of $f(z)=w$ .
Rearrange so $w$ is a function of $z$ (to discover the condition under which $w$ remains valid.

e.g., for $f(z)=\frac{1}{z-1}$ :

$\begin{align*} f(A) =&\: \left\{ \frac{1}{z-1}\::\:z\in\mathbb{C}-\{1\}\right\} \\ f(A) =&\: \left\{w=\frac{1}{z-1}\::\:z\neq 1\right\} \\ f(A) =&\: \left\{w\::\: z=\frac{1}{w}+1\::\:z\neq 1\right\} \\ f(A) =&\: \{w\::\: w\neq 0\} \\ f(A) =&\: \mathbb{C}-\{0\} \\ \end{align*}$

Domain of Combined Functions

Domain of combined functions are the intersection ( $A\cap B$ ) of the domains of all component functions and that of the combined function. e.g:

$f(z)=\frac{z-1}{z}\:,\:\: z\in\mathbb{Z}-\{0\}$

$g(z)=\frac{z}{z-1}\:,\:\: z\in\mathbb{Z}-\{1\}$

$\frac{f\left(z\right)}{g\left(z\right)} = \frac{z^{2}-2z+1}{z^{2}} \:,\:\: z\in\mathbb{Z}-\{0,\:1\}$

Domain of Composite Functions

For $f$ and $g$ with domains $A$ and $B$ respectively, the domain of $g\circ f$ is:

$A-\{z\::\: f(z)\: \notin\: B\}$

e.g., for:

$f(z)=\frac{z-1}{z}\:,\:\: z\in\mathbb{C}-\{0\}$

$g(z)=\frac{z}{z-1}\:,\:\: z\in\mathbb{C}-\{1\}$

$\text{domain of }f\circ g = \text{domain of }g - \{z\::\:\frac{z}{z-1} \:\notin\: \mathbb{C}-\{0\}\}$

$\text{domain of }f\circ g = (\mathbb{C}-\{1\} ) - \{z\::\:\frac{z}{z-1} =0\}$

$\text{domain of }f\circ g = (\mathbb{C}-\{1\} ) - \{0\}$

$\text{domain of }f\circ g = (\mathbb{C}-\{0,\:1\} )$

Inverses

Determine image set of $f(z)=w$ .
Invert $f(z)$ to find a unique $z$ in the domain of $f$ .

For $f(z)=\frac{1}{z-1}$

$f(A) = \{\frac{1}{z-1}\::\:z\in\mathbb{C}-\{1\}\}$

$f(A) = \{w=\frac{1}{z-1}\::\:z\:\neq\: 1\}$

$f(A) = \{w\::\: z=\frac{1}{w}+1\:\neq\: 1\}$

$f(A) = \{w\::\: w\:\neq\: 0\}$

$f(A) = \mathbb{C}-\{0\}$

(all same as above for finding an image set)

$z=\frac{1}{w}+1$ gives a unique soluition in $\mathbb{C}-\{0\}$ , hence $f$ has a unique inverse rule:

$f^{-1}(z)=\frac{1}{w}+1\:,\:\:\:z\in\mathbb{C}-\{0\}$

Analysis, General

Last Assignment Submitted

April 25, 2017 Adrian Leave a comment

In just over a month and a week I've submitted two 20+ page assignments. I'm exhausted.

The last section on Real Analysis was incredibly challenging. I was so short on time I realised I would've have enough time to type up the assignment for it in LaTeX, so I re-wrote all my answers neatly on paper just like the old days. In fact, I was SO tight on time, even after all this, I almost didn't make the submission. Never been so close to missing a deadline.

But overall, that whole month was incredibly stressful. I'm not sure how to avoid that kind of stress in future other than making sure I'm way ahead of the deadlines for the whole academic year. -and that's incredibly hard to do for a double-credit module like this one if you're working full-time. Yeah, that was unpleasant.

Anyway. Luckily, after all that, I had booked two weeks off for Easter. This meant my final assignment wouldn't be so much of a rush. The final assignment consisted of questions on everything from the entire academic year. There was no new material to learn for it, hence the two week deadline. Though if I hadn't taken this holiday, I don't think I would have been able to find the time to complete this last assignment. There was still a very large amount of work to do.

However... today I have submitted this last assignment too. That's it. All seven assignments complete. Material learnt. Course done.

All that's left is six weeks of revision, which will include a revision weekend off at the Open University campus in Milton Keynes. A rare chance to sit amongst fellow maths students. Although it very much isn't a break, I'll be treating it like one as I get to escape from London for a couple of days.

In fact, on the Friday I drive up I'll be stopping off at Bletchley Park! Expect photos in a few weeks...

In the mean time, I'm going to make an attempt to relax a little in my final week of vacation before going back to work and starting my revision period. Let's see if I can get my mind refreshed before the final push...

Analysis

Real Analysis Feedback

February 26, 2017 Adrian Leave a comment

As it turns out, that wasn't as bad as I thought it would be. Had some significant time constraints, and some of the concepts of continuity really threw me near the end but it wasn't a total nightmare.

Must admit though, there are still some areas which I feel I still need to "grok". (Hmm... never much liked that word... but replacing it with "understand intuitively" doesn't quite sound right either, but you know what I mean.) Concepts of continuity is one such area that I'll have to spend some extra time on in the revision stage (or maybe even just before my final Analysis section).

In summary, this was certainly the most challenging section yet. Having said that, I did manage to achieve a higher mark than I expected to get in my assignment. As usual, here are some areas in which I screwed up:

It seems intuitive to say that $0 + \infty + 0 = \infty$ , but this specific rule regarding the sum of these limits was never listed in the set that I can use, so I can't use it, hence I was marked down. I've always enjoyed working with a limited toolset, so this should come naturally after a bit of revision. The main problem is getting that full understanding of the mechanics of each rule so it can become intuitive. In fact, my answer for this particular question (as a consequence) was extremely drawn-out. The proper answer given by my tutor fits on less than half a page of A4. Hopefully more practise will let me see the quick, correct answer more quickly.

I stated Bernoulli's Inequality incorrectly. Absolutely no excuse for that. 🙁

When working out limits of formulas, always state the dominant term before reducing, and always put curly brackets around a sequence (otherwise, it's just a formula).

In some cases I was lazy and claimed that something like $\frac{3}{n+2}$ was a basic null sequence. Although it is quite obviously basic, and quite obviously a null sequence (it converges to 0 as n increases), it's not actually a basic null sequence. So even something as small as this, I need to deconstruct and prove.

Lastly, and this does bear repeating... I need a lot more practise with questions about continuity...

Next up, more group theory!

Analysis

Time Constraints

February 12, 2017 Adrian Leave a comment

I'm coming towards the end of my last section of my Analysis. I'm probably about half-way through the last book. After that, I have to answer the last question in my Analysis assignment, proof read the whole thing and submit it.

I have the whole of today, Monday, Tuesday and Wednesday before I need to submit this Analysis assignment. To make sure I can submit this assignment in time, and get ahead for my next section (Group Theory Part 2), I've taken the Monday, Tuesday and Wednesday as holiday days. That'll make a total of 5 days I've taken off work since the beginning of January just to make sure I'm where I want to be with my study.

There's a ebb and flow to where I am with my study compared to where I should be, and I won't truly understand how well I managed my time until this whole module is over in June, but I sure wasn't expecting I'd have to use holiday days to catch up on study.

One of the most frustrating things about feeling like you're behind is the nagging feeling like you don't have sufficient time to learn the materials sufficiently. This slight panic creeps in and you realise that more than anything else, you need to reach the end of the section (to be able to move on to the related assignment question). So you learn it JUST well enough to move on. Of ALL the sections for this to happen on, it had to happen with Analysis didn't it. The section I was most nervous about.

So in summary, because I've found myself short on time, I'm having to practically rush through the section on Analysis. No time for playing with concepts, no time to study the proofs in depth (or at all in some cases). Just time to get the general gist, and move on.

Something I will say is that I haven't found it necessary to keep a spider diagram of how core concepts relate to one another. Because of the structure of the learning materials I find it fairly easy to see the links and how one theory supports another proof and so on.

What has been a surprise while studying analysis is that there hasn't been a need to write any proofs in quite the same way as I was expecting. It turns out that (so far, at least) there isn't a need to have an in-depth understanding of logical notation or concepts. You need a basic understanding of the "if x, then y" structure, and the consequential converse "If not y, then not x", and so on, but not a great deal more. I'm not sure whether I'm grateful for this or not. Some of the concepts in Analysis require all my brain power, so I'm not sure the additional logical puzzles on top of that would help. Though on the other hand, having a decent foundation in logic feels quite important. I suppose, again, I'll have formed a more solid opinion on this by the end of the module.

Analysis, General

Analysis Battle

March 23, 2016 Adrian Leave a comment

It turns out that wrapping up a permanent job and starting a new one takes an enormous amount of time. Throw a holiday or two into the middle of it and you suddenly completely lack any spare time whatsoever.

Glad to say I'm back now though. Ready to tackle the final assignment of my intro module, and close things off for a Summer (of Analysis study).

Speaking of Analysis, I've spent a few more lunch hours running through the exercises of the end of Chapter 1 on the real number system and even after ALL the reading I've done I'm only able to complete about 50% of the questions. I feel my knowledge is lacking enormously. What makes things more frustrating is that David Brannan's book doesn't contain any solutions for the exercises at the end of each chapter. So I'm completely unable to unstick myself (or check to see if I've answered the question in the correct way).

As a consequence I feel like I'm slightly wasting my time with this book. Just banging my head against another dead-ender of a question. This is extremely unfortunate, as I was looking forward to finally working through as much as possible before September. Hoping it would give me an edge for my next module. But today, I tried to think about the situation logically: It feels as if I'm lacking knowledge. Knowledge and experience. There haven't been nearly enough examples in this book for me to get a feeling for the kinds of things I should be proving. So maybe that's what I need... more examples... more simple questions to attempt.

There was only one source I could think of that may deliver this... On the maths forum, I was given a link to proof exercises as supplied to kids studying pure mathematics at a-level. This might just give me a leg up...

Analysis, General, Proofs

Readjusting Learning Methodologies

November 18, 2015 Adrian Leave a comment

I've just finished reading Lara Alcock's book on how to learn about Analysis. Or rather, I've finished reading the first part, and the part on the real number system.

Overall, the book has led me to reconsider my current learning technique. So much so, I've compiled a list of steps to follow depending on whether I read about a new definition, theorem or proof.

In turn, this has made me realise I may benefit from starting my main book on Analysis again from the beginning, but applying these new steps as I go. After all, I am still only at the beginning (kind of), and I don't have any kind of deadline looming over me (which is really nice). Overall it seems like the perfect opportunity to try out some new learning methodologies!

Out of the handful of additions, there are two really big changes for me.

The first being mind maps. As I go through my Analysis, I'll be creating a mind map of concepts, seeing how one builds on another. I'd tried to use mind maps before at university and they'd largely proved completely useless. Here, however, mind maps appear to offer a perfect way to visualise the building of concepts into larger concepts. Here's the beginning of my first mind map!

I'm using draw.io as the tool of choice. It seems flexible enough for what I need it for, it can save as XML, and it supports mathematical notation! (mathjax latex formatting I believe)

The second big change to my learning involves learning by self-explanation. This technique, mentioned in Lara Alcock's book, appears to be one of the key processes involved in truly understanding and appreciating Analysis. You can find out more about self-explanation training from Loughborough University's Mathematics Education Centre website. My difficulty here will lie in concentrating on actually doing self-explanation, rather than just paraphrasing (turns out, it's a very easy trap to fall in). So long as I do it regularly enough, self-explanation will be more likely to come to me naturally.

Expected result: More effective learning and better notes!

Analysis, Text Books

Books For Understanding Books

October 30, 2015 Adrian Leave a comment

I couldn't help myself.

I've bought another book.

The reason I bought it is to help me with the book I'm currently reading... but it's not as bad as it sounds.

The last Analysis query I had, I posted to the OU forums. As usual, my question was answered almost instantly in a concise and understandable way. Awesome!

However, there was another post a few days later suggesting that I read "How To Think About Analysis", another book by Lara Alcock.

Initially I thought it would be a bad idea to drop my current book about Analysis, and pick up a new one, but it turns out that after the first 50 pages, this book can be used as a companion to learning different sub-topics of Analysis. Specifically, after the first 50 pages, the remainder of the book is split into sections about Real Numbers, Sequences, Series, Continuity, Differentiability, and Integrability. Each sub-topic appears to be about 40-ish pages long, and can be read just before or during the actual study of each. Bite-size!

Although I've not quite finished the first section yet, I've already added several new strategies to my set of learning techniques. Despite the fact that the knock-on effect is that the learning process may become slower, the idea is that my knowledge and understanding of the material will become much much deeper.

I'll try and give another review once I've completed the first part, the section on real numbers, and related it all to where I currently am in my larger Analysis text book.

Analysis, Maths, Proofs

Proof of Inequalities by Mathematical Induction

October 2, 2015 Adrian Leave a comment

Still reading though my book in Analysis, I've come across a section on proving inequalities. I'm glad to say that all of this made sense... until I reached a sub-section on proving an inequality by mathematical induction.

As I've written previously, I find that proofs are notoriously unintuitive. In the past however, I have been particularly puzzled by the logical steps involved in proving an inequality by mathematical induction.

To explain my difficulties, let's have a look at the example provided in the book:

Prove that $2^n \geq n^2$ , for $n \geq 4$ .

If we're proving this by mathematical induction, we generally follow these steps:

Let $P(n)$ be the statement $2^n \geq n^2$ .
Show that $P(4)$ is true.
Assume that $P(k)$ is also true for $k \geq 4$ .
Show that $P(k) \Rightarrow P(k+1)$ . Or rather, show that if $P(k)$ is true, then $P(k+1)$ is also true.

Step 4 is the key step here in the proof as it shows that if any number is true, and the next number is also true, then you can apply this rule forever, and your original statement must be true for all numbers!

Anyway, lets jump to step 2. Show that $P(4)$ is true. Well if $n=4$ , then $2^4 = 16$ and $4^2 = 16$ . So $P(4)$ is true! Easy.

Let's look at step 3. Let's ASSUME that $P(k)$ is true for some $k \geq 4$ .

Now, this is the part that caught me by surprise... At this step, the text in the book reads as follows:

"So, we are assuming that $2^k \geq k^2$ . Multiplying this inequality by 2 we get:

$2^{k+1} \geq 2k^2$

,

so it is therefore sufficient to prove that $2k^2 \geq (k+1)^2$ ."

Wait, what? How is it that all of a sudden, all we need to prove is that $2k^2 \geq (k+1)^2$ ? This isn't explained explicitly in the text so I had to close the book and do a bit more thinking.

First thing I had to realise here is that the "Step 4" I've listed above requires a bit more detail... What you're actually trying to do is show that you can progress naturally from $P(k)$ to $P(k+1)$ . ie: We should be able to show that we can progress naturally from:
$2^k \geq k^2$
to:
$2^{k+1} \geq (k+1)^2$ .

Now, if we multiply $2^k \geq k^2$ by 2, as mentioned in the text, we do arrive at:
$2^{k+1} \geq 2k^2$

This is good, as we've managed to get the $2^{k+1}$ we were looking for on the left-hand side of the inequality. But the right-hand side looks nothing like the right-hand side of $P(k+1)$ ie: $(k+1)^2$ .

Here's the key though... It doesn't matter they they're not the same. We only need to see how $2k^2$ and $(k+1)^2$ relate to each other. Look back at Step 3. Part of this assumption is that $k \geq 4$ . Just as a test, let's try $k=4$ :

$2k^2 = 2 \times 4^2 = 32$
and
$(k+1)^2 = (4+1)^2 = 25$

Well this is interesting. It's looking as if $2k^2 \geq (k+1)^2$ . This is exactly what was written in the text!

But to really ram it home, what we really have now is the following:

$2^{k+1} \geq 2k^2 \geq (k+1)^2$

So.... this show us that IF we can prove that last bit $(2k^2 \geq (k+1)^2 )$ is true for all $k \geq 4$ , and not just $k=4$ we have managed to prove that we can get from $P(k)$ to $P(k+1)$ !!! This is exactly why the text in the book said "so it is therefore sufficient to prove that $2k^2 \geq (k+1)^2$ ."

I'm sure in future I'll jump on this immediately and say "oh yes, of course that's all we need to do now", but working through the derivation of why it was sufficient was extremely useful. Long-winded... but useful.

Ah, the learning process...

Analysis, Text Books

Year Four Begins!

September 17, 2015 Adrian Leave a comment

My new learning materials have finally arrived!

This is the amount of reading and exercises that I would normally have to work through over a nine-month period. Entirely doable.

However, as I've mentioned in previous posts, this module is merely to make up the credits for my first stage. Bad news is: it's all quite basic. As a result, I'll also be working through a nice fat book on analysis, to ease me in to my second stage that starts next year. As such, my nine-month work load actually looks a little more like this:

So we'll see how far I get with all that!

Flicking through the first couple of pages of these new materials, I realise that they cover some very basic areas of mathematics indeed. Perhaps even a little more basic than I was expecting. I think I'll have to keep reminding myself that this was my plan from the beginning, and just concentrate on submitting my assignments on time. This work will definitely be taking a back seat...

More importantly, over the past couple of weeks I've also been working through the book on analysis, and although I'm only a few pages in, it's proving to be really valuable; for one, I'm becoming a lot more comfortable with proofs and solution sets of inequalities.

Image Sets

Domain of Combined Functions

Domain of Composite Functions

Inverses

…is learning mathematics.