Monthly Archives: September 2020

Analysis, Complex Analysis, Proofs, Pure Maths

Complex Functions: Domains, Image Sets and Inverses

I can imagine having to refer to these notes regularly, so I'm putting them here!

Image Sets

  1. State the domain 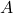A of f(z)=w.
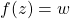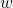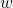  2. Rearrange so w is a function of z (to discover the condition under which w remains valid.

e.g., for f(z)=\frac{1}{z-1}:

    \begin{align*} f(A) =&\: \left\{ \frac{1}{z-1}\::\:z\in\mathbb{C}-\{1\}\right\} \\ f(A) =&\: \left\{w=\frac{1}{z-1}\::\:z\neq 1\right\} \\ f(A) =&\: \left\{w\::\: z=\frac{1}{w}+1\::\:z\neq 1\right\} \\ f(A) =&\: \{w\::\: w\neq 0\} \\ f(A) =&\: \mathbb{C}-\{0\} \\ \end{align*}

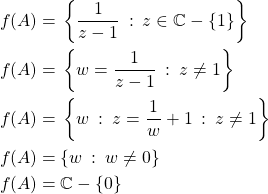
Domain of Combined Functions

Domain of combined functions are the intersection (A\cap B) of the domains of all component functions and that of the combined function. e.g:

f(z)=\frac{z-1}{z}\:,\:\: z\in\mathbb{Z}-\{0\}

g(z)=\frac{z}{z-1}\:,\:\: z\in\mathbb{Z}-\{1\}

\frac{f\left(z\right)}{g\left(z\right)} = \frac{z^{2}-2z+1}{z^{2}} \:,\:\: z\in\mathbb{Z}-\{0,\:1\}

Domain of Composite Functions

For f and g with domains A and B respectively, the domain of g\circ f is:

A-\{z\::\: f(z)\: \notin\: B\}

e.g., for:

f(z)=\frac{z-1}{z}\:,\:\: z\in\mathbb{C}-\{0\}

g(z)=\frac{z}{z-1}\:,\:\: z\in\mathbb{C}-\{1\}

\text{domain of }f\circ g = \text{domain of }g - \{z\::\:\frac{z}{z-1} \:\notin\: \mathbb{C}-\{0\}\}

\text{domain of }f\circ g = (\mathbb{C}-\{1\} ) - \{z\::\:\frac{z}{z-1} =0\}

\text{domain of }f\circ g = (\mathbb{C}-\{1\} ) - \{0\}

\text{domain of }f\circ g = (\mathbb{C}-\{0,\:1\} )

Inverses

  1. Determine image set of f(z)=w.
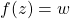  2. Invert 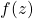f(z) to find a unique z in the domain of 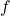f.

For f(z)=\frac{1}{z-1}

f(A) = \{\frac{1}{z-1}\::\:z\in\mathbb{C}-\{1\}\}

f(A) = \{w=\frac{1}{z-1}\::\:z\:\neq\: 1\}

f(A) = \{w\::\: z=\frac{1}{w}+1\:\neq\: 1\}

f(A) = \{w\::\: w\:\neq\: 0\}

f(A) = \mathbb{C}-\{0\}

(all same as above for finding an image set)

z=\frac{1}{w}+1 gives a unique soluition in \mathbb{C}-\{0\}, hence f has a unique inverse rule:

f^{-1}(z)=\frac{1}{w}+1\:,\:\:\:z\in\mathbb{C}-\{0\}

Pure Maths, Research

A New Year of Study Begins!

September has come around already!

My virology work placement came and went so quickly. Great experience. I was certainly not expecting it to be such a creative process. Or should I say "necessarily creative process". It seems with research like this, you really do need to be mindful of other results popping out of your work. If the tangent appears to be more important/meaningful than the original work, then it's best to follow it!

Of course this creative approach gives rise to a bit of a problem. The project has the potential to meander. I suppose this would be fine on a longer time scale, but for my all-too-brief 8 weeks it meant I wasn't able to neatly draw a line under it by the end of the placement.

Though having said that, the work that I was looking at wasn't time-dependant so I still have however long I want to complete the project in my spare time. After this next year of study I'd love to return to it.

Speaking which... my next year of study has started! I won't be informed of my assigned tutor for about another month, but I have my learning materials. So learning has begun! This year it's complex analysis. Very excited to be looking at this subject, and to be writing up the areas I have difficulty with on here.

(Side note: Wow, I've been writing on this blog for 5 years?!)