So I've finally completed all my assignments! I've just had the very last one returned to me and again, although I did well, there are very obviously some areas for improvement:

 

Models for Populations

Very small thing here, but when asked to describe the shape of the age-specific death rate, it's important to describe it in terms of the rate (of change).

 

Genetics

Wow. My weakest area by a long way here... It'd be wise for me to avoid any exam questions on genetics... But for the moment, let's examine what I did wrong to try and understand the assignment questions better at least. (It's mainly an issue with conditional probabilities).

Proportions

When calculating the probabilities of genotype combinations of parents, if you're given the genotype of one parent you don't need to use it in the calculation! eg: Despite the proportion of a genotype in a population being 0.2, if you're given the genotype of one parent, then the chance of them being that genotype is 1.0, not 0.2! Making a mistake like this obviously has a knock-on effect on working out probabilities for the children's genetics, insofar as the probabilities of the children will be incorrect too.

But I compounded my issue with the children. It took me a while to review the next bit to work out where I went wrong, but here we go...

When working out the parent-child genetics, you start by working out two sets of probabilities:

1. The probability of the parents being certain combinations of genotype (easy in this specific case, as the probability of one parent is 1.0). The probability of the parent of unknown genotype follows from the Hardy-Weinberg law. We'll call the probability of all the mating types .
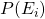2. The offspring probabilities, which follow from Mendel's first law. Though we'll talk about them in terms of phenotype, so 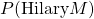means the probability of Hilary being of phenotype M.

So the next question asked just that: What is the probability of Hilary being phenotype M (which was just one genotype "MM").

This question I managed to get correct based on my initial incorrect probabilities of the parents, but it's important to explain it for the next question. So it turns out that:

So you multiply each offspring probability, (the probability of Hilary being phenotype M given the mating type) with the associated mating type probability. And you sum them across all mating types. Easy.

But the next question was:

Calculate the probability that sisters Hilary and Jane both have phenotype M. This was the bit that I got completely wrong that took me a while to review. I ended up squaring the result I got from the last question. Very not correct. 🙁 From the above, we know we start with:

and it turns out:

Which suddenly makes it all very very clear. I suppose this goes to show that when you come across something convoluted, it's worth taking extra time out to run through it in depth and make detailed notes on it. Doing so here would've paid off. I think the problem I have with genetics questions is that there are quite a number of ways in which these questions can be phrased.

 

Writing Conditional Probabilities

Well this went really wrong. This is probably my weakest area, and is related to the above slip-ups in the questions with Hilary and Jane.

"Show the that proportion of male offspring for the second mating that you should expect to have plain wings (gene contains dominant allele A) is ."

Here, I wrote the definition incorrectly, but calculated the correct result. Kind of double-bad. 🙁 Here, I wrote:

P(male A)
(which is the joint probability of a male having the allele A)

When I should have written:
P(A | male)
(the conditional probability of offspring having the allele A given that they're male.)

 

The Hardy-Weinberg Law

A lengthier title to this subsection would be: "When to calculate the proportions of subsequent generations of a certain type using Hardy-Weinberg, and when to use your own table of probabilities".

As above, the table of probabilities includes the probabilities of the parents of certain types mating, and the probabilities of the associated offspring genotypes.

The question:

"One male and one female are chosen at random from all the offspring of the mating, and are themselves mated. What is the proportion of female offspring of the second mating to have a dominant allele?"

In this case, there were two genotypes which had a dominant allele, AA and Aa. But how do I parse this question? This question is asking about grandchildren of the initial parents! It's also asking about "proportion" which hints that I should be using Hardy-Weinberg proportions. Turns out not. It seems that you can only use the Hardy-Weinberg law when you're given the proportion of three genotypes of a starting generation.

So what are we left with?

P(AA | female) AND P(Aa | female)

Which in this case is equivalent to:

Notice how this differs from the sum in the last section (the Hilary and Jane example), because there's no assumption made about them both having the same father.

Last related one here that tripped me up was:

"What is the proportion of dominant-alleled females in this second mating would you expect to be AA?"

Again, I used the Hardy-Weinberg law to calculate this, when I should've been using conditional probability.

So it seems I needed to go through the process of parsing the question, and translating it into stats language: "What's the probability of offspring being genotype AA given that they're a female with a dominant allele?". The probability we require here is:

P(AA | dominant allele female)

Using the standard, straight-forward rule for conditional probability I learned in my first section back in September, this is equivalent to:

What's the numerator here? The probability of being AA and a dominant-allele female? Well yeah, AA is dominant, we know that. So this is just the probability of being AA and female:

It's just one part of the previous question.

Then what's the denominator? The probability of being (proportion of) a dominant-allele female generally? So AA female and Aa female?  Well that was the actual answer to the last question!

So that's it. There's a lot of parsing that needs to be done generally:

Have I been given proportions? Use Hardy-Weinberg.
No proportions? Use a table of parents and offspring probabilites.
What am I given, what don't I have to calculate?
What are they asking me, is the probability conditional?
If it's conditional, I can separate it out but then I need to parse what each of these new probabilities mean.

Armed with this little checklist, I may have done a bit better in my genetics questions!

General Stuff

Range

If your answer is an equation in terms of x, always state the range of possible values of x:

Variance

Annoying oversight here. When stating the variance of the lifetime of something was 42.92 months, I should've said it was 42.92 . Not often you think of months-squared, but here, it's relevant. Variance!

Log and Ln

Concentrate when typing one or the other into your calculator. There's a big difference, people... Thankfully I only slipped up once here.

 

And that's it! Now it's just revision time until my exam on the 8th of June. Of course, due to our new friend covid-19, I'll be taking my exam at home which will be a bit weird. Plenty to revise though, so I'll get started...

 

Two thirds of the way through my assignments!

Again, fairly happy with the mark I received for this, but there were some aspects of this assignment I found challenging, and some where I thought I might've done quite well on, but slipped up in some way.

Let's cover some areas here:

Finding A Real-World Process

For these questions I had to find a real-world process that could be modelled with the given mathematical objects/processes. Kind of the opposite of a mathematical modelling problem.

I found these tasks really difficult. What I found to be the worst aspect about getting this kind of question wrong is that it's not necessarily my understanding of the mathematical process that's flawed. I feel in each of these cases, I did my best to find a real world example, knowing that the example I gave, itself, was slightly flawed. So despite the fact that I can perfectly explain each mathematical process, I couldn't explain how each could be applied to a real world process so lost marks.

The two models were the Galton-Watson branching process, and the simple random walk (specifically, a particle executing a simple random walk on the line with two absorbing barriers).

The two typical examples that are referred to in my texts are genetics and mutations for the Galton-Watson branching process:

"A mutation is a spontaneous transformation of a particular gene into a different form, and this can occur by chance at any time... The mutant gene becomes the ancestor of a branching process, and geneticists are particularly interested in the probability that the mutation will eventually die out."

For the simple random walk, the example of the "gambler's ruin" was given. Imagine two people with £10 each, each of them betting on an event. If one of the two loses the bet, they give £1 to the other (the random walk on the line). If one of them runs out of money, then they lose (one of the "absorbing barriers" are hit).

In coming up with answers, I could've used Google, but that would've been cheating. However, now I've completed the assignment and received my grade, Google is my best friend in finding suitable answers here...

Seems you can use the Galton-Watson branching process to determine the extinction of a family name, and I found a good example of a random walk with absorbing barriers in this MIT paper, featuring a little flea called Stencil. It discusses the probability of him falling over the Cliff of Doom in front of him, or the Pit of Disaster behind him.

 

Concluding An Answer

A couple of my answers here and there were classed as being incomplete. Generalising each case:

1)
Upon finding that an answer resembles a certain construction (a probability distribution function, cumulative distribution function or generating function), as well as saying which distribution the function belongs to, you should also explicitly state the variables that appear in it. Even to anyone non-mathematical, it would be obvious to see that the variables in the general case are associated with the specific answer you arrived at. Though for assignments (and exams, presumably) this is not enough. If a general function has variables explicitly state what each one is in your answer.

eg: the p.g.f. of the modified geometric distribution is

If your answer resembles this, say what a, b, c and d are.

In addition, if your answer is a probability (or set thereof), include a statement describing them.

Note that one whole mark can be deducted for an insufficient conclusion (apparently).

2)
Don't forget your definitions.

Specifically:

To calculate the variance of the position of a particle (along the random walk line) after n steps, you can just sum the variances of each step. However this only works because each individual step is independent of the last (one of the properties of the random walk). Due to the fact that I didn't mention this definition of the variance of a particle in a random walk, I lost half a mark. Not massive, but where you can mention a definition, mention it.

 

Different Routes In A Markov Chain

I struggled with this, and although I arrived at the correct answer, the method I had used was entirely wrong (and also a little inelegant).

In this question, I covered all routes separately and so had a small handful of different probability calculations. Though when considering potential routes in a Markov chain, you can consider all routes simultaneously by taking advantage of something called an absolute probability (of the Markov chain being in a particular state at a particular time), given an initial distribution. (for my own reference this is covered in Book3, Subsection 11.2, p.87. And the handbook, p.23 item 17).

 

Arbitrary Constants

Does it matter if an arbitrary constant is positive or negative? (my ref: Q6a). I previously thought not. In this instance my constant in an integral calculation absorbed the negative sign that was in front if it. After all, a negative general constant is still a general constant, right? Well I lost half a mark here because of the absorption, and it's not currently clear why. I've asked my tutor, and I'll update it on here once I hear back from him.

Very happy with the high mark I achieved for this first assignment. Though as usual, there's a decent about to be improving. Let's start by looking at some of the more major things my tutor pointed out.

Variance

First thing is variance. How do you calculate it? Well it turns out there are a couple of ways. I just decided to use the most cumbersome way...

Calculating the mean (expectation ) is easy. Multiply each number with its probability and sum them all:

The variance can then be calculated in one of two different ways:

or

When they're written out like this, it's fairly obvious to see which method is more like the method used to calculate the mean and as  such would be far less hassle. ( is an integer and and can be reals/rationals).

 

Multivariate Poisson Process

This was the question in which I lost the most marks:

Customers arrive at a shoe shop according to a Poisson process with a rate of 20 per hour.
15% of customers buy men's shoes.
60% buy women's shoes.
25% buy children's shoes.
Calculate the probability that exactly eight customers arrive in half an hour, exactly three of whom wish to purchase children's shoes.

This is such a typical mistake for me to make in statistics. I'm sure I've made this kind of mistake before...

What I ended up doing was working out the probability of the number of customers being 8 using the Poisson distribution's probability function. This was fine.

Then I used the same probability function to find the probability of 3 people wanting to buy children's shoes and multiplied them together. Wrong. At this point I needed to find the conditional probability that of the 8 customers, 3 bought children's shoes. Hence, here I shouldn't have used the Poisson distribution, I should've used the Binomial distribution instead. ie: from 8, choose 25%.

Reflecting back on the question, the correct answer seems slightly more obvious now. Especially given the "...exactly three of whom..." part of the question. I struggle to be mindful of stuff like this in the moment of answering a stats question. I suppose this part of the "translating English into maths" issue comes with more practise...

Index Of Dispersion

Again, my issue here was to not observe subtleties in the question. Given information about the associated distributions, I was initially meant to calculate the mean and variance of the total number of books bought in 9 hours. I managed to get this first part right, but the second part of the question asked me to calculate the index of dispersion for "this process". It turns out that "this process" refers to the process in the main question generally and not the process of books being bought within 9 hours. In this instance, ignoring the total number of books bought in 9 hours (kind of) simplifies the answer too.

Other Issues

In this first assignment, I lost a half a mark here and there for incorrect arithmetic. (GASP!). Upon completing my draft submission, instead of just reading through it, I should sit down and verify all my working. It will take more time, but if it scrapes 2 marks back, it could be worth it.

Other issue that occurred more than once was a lack of units when talking about rates of things happening. So there's a requirement to state " per hour" instead of just "".