Another brutal chapter. Brain was pushed to the limits with this one.

First chapter was "new metrics from old", about how sets and distances can be combined to form new metrics. Second was "the Cantor metric" (Cantor space, just being what is essentially a binary tree). Next was "equivalent metrics", that involved a lot of inequalities. Fourth was "spaces of functions" which covered sequences of functions and their limits (different from sequences and limits). Lastly was "the max metric on ". Conceptually, this was a jump as is actually the set of all continuous functions that map from to 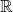. Had some really tricky questions in that last section. The majority of my brain power went into understanding how to prove that the function you apply to functions when you integrate is continuous. Exhausted.

On to the next chapter.

Again, this chapter was fairly merciful. First section was a natural progression from the last chapter, namely continuity of functions from 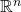to 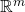and a return to the all important triangle inequality from my complex analysis module last year.

Next section was great as it introduced a new mathematical object: the metric. Always fun, learning about something new like this. Though something that really tripped me up (that I feel I'm still struggling with now) is the geometry of metric spaces. There are sets defined around points in spaces called "balls", be it open or closed. I seem to have a big problem with defining what are inside and outside of these circular (in 2D) sets based on their defined radii. Sounds simple, but it seems it's not very intuitive. Not being able to define what's in your set is bad, so I need to do some further reading on this.

Next up was sequences in metric spaces, followed by the definition of continuity in metric spaces.