My first unit is done! I managed to find time to complete the first assignment too. This is timely, as the course officially starts tomorrow.
This unit was interesting. Looking at the title "differential equations" I thought "Oh, okay, fine. I've done this before". Then opening up the book, I realised "Oh wait. I haven't quite done THIS before". That's when the fear crept in... how much of a learning curve would I be facing in this new unit?!
Forging through, I had to concede defeat on one or two examples, but I came out the other end confident about all the material I'd covered. Only now I've completed the assignment do I feed confident about my ability on the subject matter, but it's also one of those areas where I need to keep up the practise.
All too often, it's the first unit that you return to at revision time and think "what IS all this?!". It's been hinted at that themes of second order differential equations reoccur throughout the module so I'm hoping I'll stay in practise.
So I'll give the assignment a final proof-read and then submit it tomorrow on the first official day of the module. Good start.
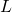 is regular.
is regular.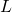 .
.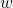 s.t.
s.t. 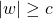 .
.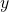 s.t.
s.t. 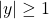 .
.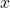 s.t.
s.t. 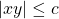
 .
.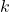 s.t. the resulting string is not in
s.t. the resulting string is not in 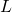 .
.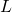 is regular and
is regular and 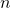 is the number of states.
is the number of states.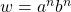 . Thus
. Thus 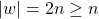 .
.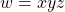 , where
, where 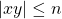 .
.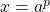 ,
, 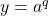 , and
, and 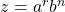 , where
, where 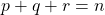 ,
, 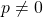 ,
, 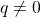 ,
, 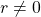 . Thusly
. Thusly 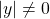 .
.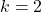 . Then
. Then 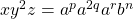 .
.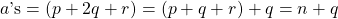 .
.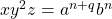 . Since
. Since 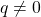 ,
, 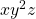 is not of the form
is not of the form 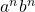 !!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!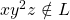 . Hence
. Hence 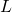 is not regular.
is not regular.
