So that's it! The Summer has ended!
How far has my extra study got me? Well I've managed to get through around 120 pages of "How To Prove It" by Velleman, and have generated just over 70 double-sided pages of A4's worth of exercises from the book. Not bad for an extra-curricular topic!
This book has helped me loads. It's succeeded in taking away a lot of the mystery involved in reading and writing proofs.
Every topic in the book up until now has flowed well, and allowed me to think about solutions to the various problems fairly naturally. What I mean by that is, I never became absolutely stuck and unable to answer a question.
Having said that, the sub-topic I'm finishing on is proofs involving quantifiers. This is the one area in which I'll admit I've been struggling. At this point in the book, I've learned so much about the number of ways in which to decon/reconstruct a problem that any possible method by which to prove a theorem has actually become less obvious.
Here's an example of how convoluted the scratch work of a basic proof has become. Here's question 14 from p.122:
Suppose 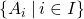 is an indexed family of sets. Prove that
is an indexed family of sets. Prove that 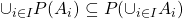 .
.
It's a short question, but this immediately looks like a nightmare to a beginner like myself. We've got a mix of indexed sets, a union over them, and power sets.
First off I need to properly understand the damn thing. Seems sensible to draw up an example using the theorem...
Let's say 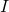 is
is 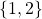 . So we've got
. So we've got 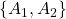 .
.
Now let's say that 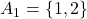 and
and 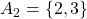 .
.
Looking at the LHS of the thing I need to prove, it's actually pretty easy to break down:
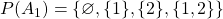
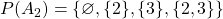
Which means that the union of all the elements of the power sets of 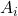 is:
is:
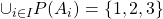
A little half-way recap: the theorem says that in my example, 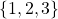 should be equal to, or be a subset of
should be equal to, or be a subset of 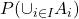 (the RHS).
(the RHS).
Let's see if that's true shall we?
Within the parenthesis of the RHS we've got  . So this is the union of all elements of all indexed sets. In this example:
. So this is the union of all elements of all indexed sets. In this example:
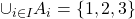
Only thing missing now is the power set of this:
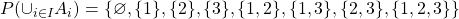
And there we go. Now I understand exactly what the theorem means. 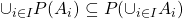 , in this specific example, turns out to be :
, in this specific example, turns out to be :
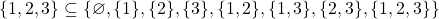
which is obviously true. Theorem understood. Achievement unlocked. Tick.
As recommended by Velleman, I'll also try to construct the phrasing of the proof along-side the scratch work as I go. Like so:
Suppose a thing is true that will help to prove the theorem.
[Proof of theorem goes here]
Thus, we've proved the theorem.
Okay, let's start.
The theorem means that if 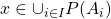 then
then 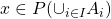 . So one thing implies the other. We can then class
. So one thing implies the other. We can then class 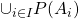 as a "given", and aim to prove
as a "given", and aim to prove 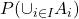 as a "goal". So blocking out our answer:
as a "goal". So blocking out our answer:
Suppose that 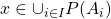 .
.
[Proof of 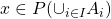 goes here]
goes here]
Thus, 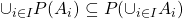 .
.
So let's start analysing 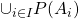 , remembering not to go too far with the logical notation. With baby steps, the definition of a union over a family of sets (here, the outer-most part of the logic) is:
, remembering not to go too far with the logical notation. With baby steps, the definition of a union over a family of sets (here, the outer-most part of the logic) is:
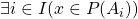
Then, going one step further, using the definition of a power set:
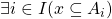
Now we could go further at this point, applying the definition of a subset, but I'll stop the logical deconstruction here. In this instance, I've found that if I keep going so the entire lot is broken down into logical notation it somehow ends up getting a bit more confusing that it needs to be.
With this as our given, I notice the existential quantifier. Here, I can use "existential instantiation" to plug any value I want into 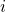 and then assume that what follows is true. So at this point the new "given" is simply:
and then assume that what follows is true. So at this point the new "given" is simply:

Nice and simple.
Let's update the outline of our proper proof answer:
Suppose that 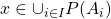 .
.
Let 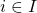 be such a value that
be such a value that  .
.
[Proof of 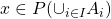 goes here]
goes here]
Thus, 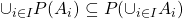 .
.
So let's now move on to our "goal" that we have to prove: 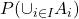 .
.
Again, starting from the outside, going in,
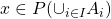
by the definition of a power set becomes:
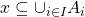
I can't do a lot with this on it's own so I'll keep going with the logical deconstruction. By the definition of a subset, this becomes:
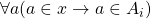
So now, using "universal instantiation" I can say that here,  is arbitrary (for the sake of argument, it really can be anything), and that leaves us with an updated "givens" list of:
is arbitrary (for the sake of argument, it really can be anything), and that leaves us with an updated "givens" list of:

and
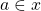
and a new "goal" of
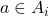
Hey, but wait a sec... Look at our "givens"! If  is in
is in 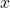 ... and
... and 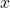 is a subset of
is a subset of 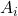 , then
, then  must be in
must be in 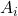 ! -and that's our goal!
! -and that's our goal!
So update our proof:
Suppose that 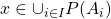 .
.
Let 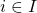 be such a value that
be such a value that  .
.
Let  be an arbitrary element of
be an arbitrary element of 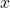 .
.
[Proof of 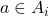 goes here]
goes here]
Therefore 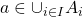 . As
. As  is arbitrary, we can conclude that
is arbitrary, we can conclude that 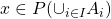 .
.
Thus, 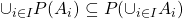 .
.
So let's wrap this up.
Theorem:
Suppose 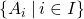 is an indexed family of sets. Prove that
is an indexed family of sets. Prove that 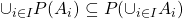 .
.
Proof:
Suppose that 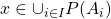 . Let
. Let 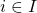 be such a value that
be such a value that  , and let
, and let  be an arbitrary element of
be an arbitrary element of 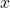 . But if
. But if 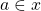 and
and  , then
, then 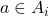 . Therefore
. Therefore 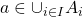 . As
. As  is arbitrary, we can conclude that
is arbitrary, we can conclude that 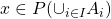 . Thus, we conclude that
. Thus, we conclude that 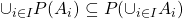 .
. 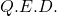
Overall the task has involved unravelling the symbols into logic, making sure they flow together, and then wrapping them back up again.
See what I mean by convoluted? All that work for that one short answer. I must admit, I still don't know if my reasoning is 100% correct with this. Despite some parts of this seeming simple, this really is the very limit of what I'm capable of understanding at the moment. I picked this example to write up, as so far I've found it to be one of the most complicated.
The next section of the book seems to marry this quantifier work with another previous section about conjunctions and biconditionals, that I found to be quite enjoyable at the time. Then towards the end of the chapter, Velleman seems to sneak in some further proof examples using the terms epsilon and delta. I imagine this is a sneaky and clever way to get the reader comfortable with further Analysis study...
Alas, my study of Velleman's book will have to stop here. I understand a lot more than I did, though not everything there is to know. I feel it may be enough to give me a slightly smoother ride through my next module, which was the whole point of me picking this book up. It's been so good, I hope I have a chance to return to it. I feel later chapters would put me in an even better position for further proof work!
For now... the countdown begins for the release of my next module's materials!





