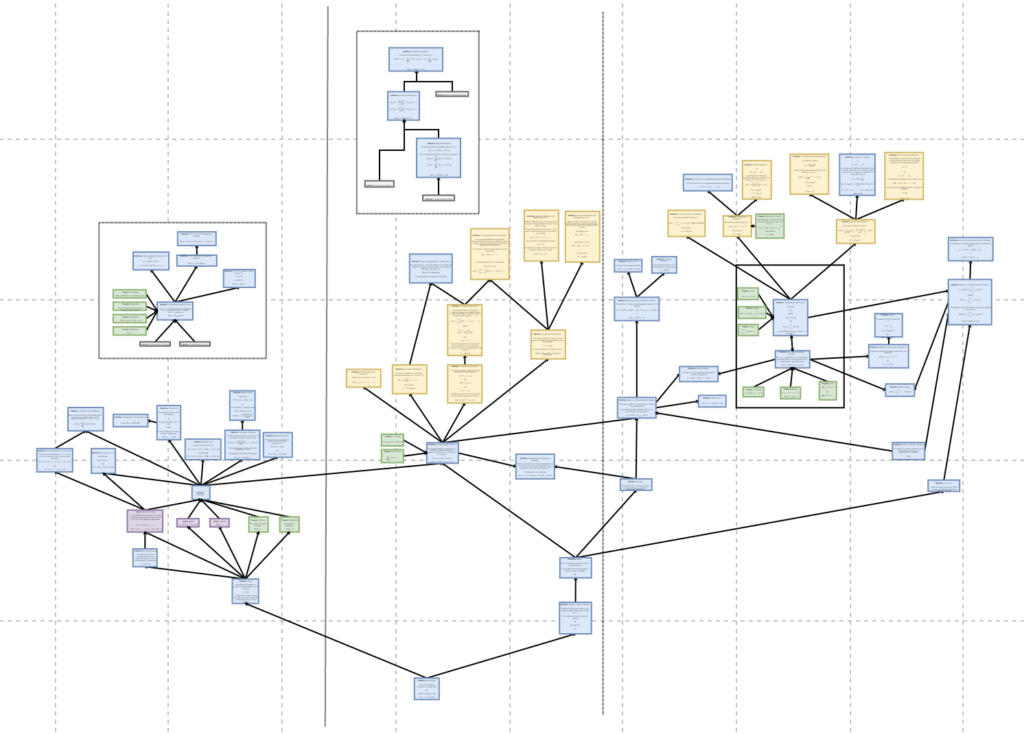
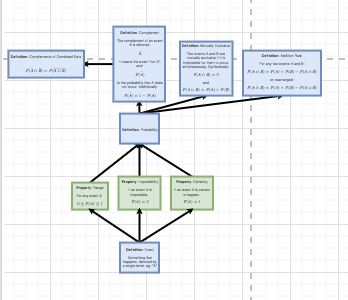
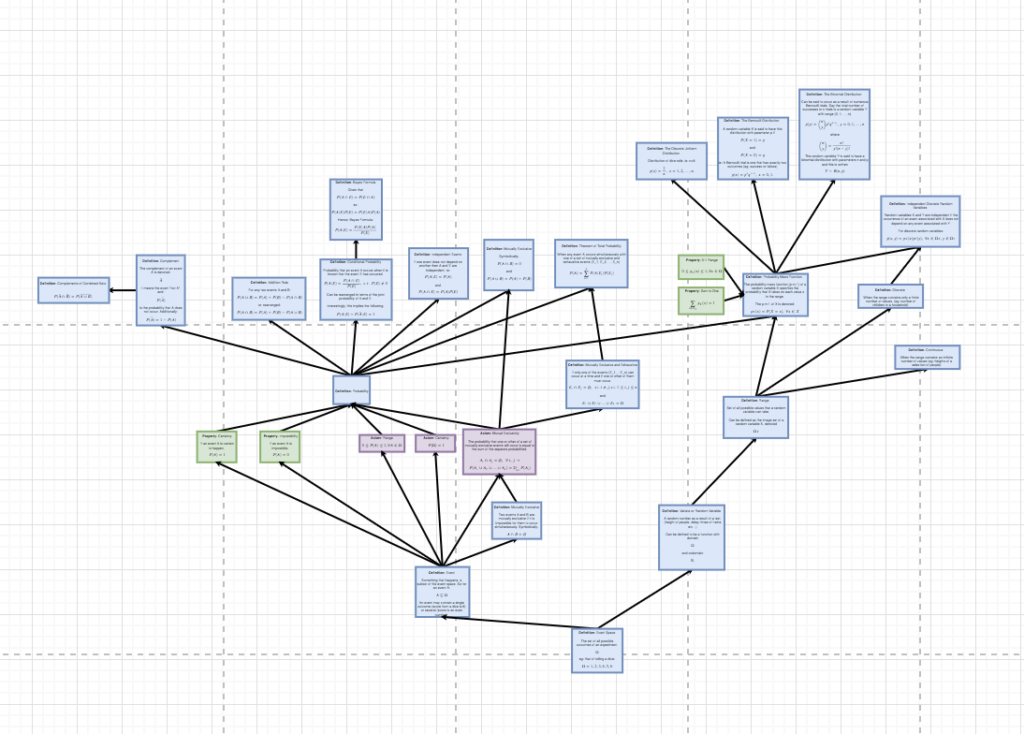
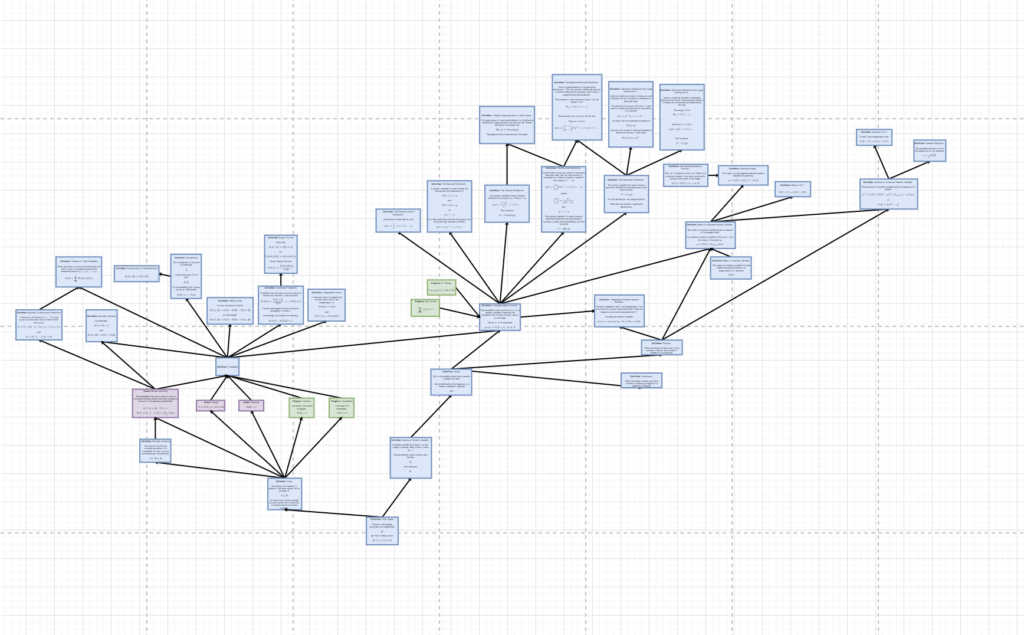
Now, looking at the other integral from Oct 13th...
![]()
In my opinion, this was scarier than the first, but looking at it again, what makes it scary is the various powers. e to the power of x to the power of 2 and such.
But why should this be scary? There's practically only one tool that one could use to solve this: the only tool that includes functions of functions, integration by substitution:
![]()
In our case, the inner function:
![]()
so:
![]()
and the outer function:
![]()
Plugging all these into our "integration by substitution" tool gives:
![]()
But this is slightly different to the original integral due to that minus sign. Of course this is trivial to deal with as:
![]()
Great! So now we have the structure we require to apply integration by substitution! We can substitute all of that with ![]() , and all the scary bits go away. So:
, and all the scary bits go away. So:
![]()
![]()
![]()
![]()
![]()
![]()
Then substituting ![]() (=
(=![]() ) back in:
) back in:
![]()