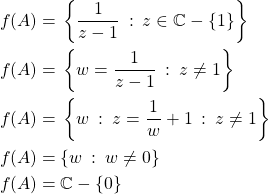My first complex analysis assignment has been marked and returned. I don't think I've ever felt the urge quite so much to learn from my mistakes.
Consequently there has been quite a lot of post-assignment learning... :/
This assignment featured a very brief introduction to complex numbers as a refresher, then broadly covered complex functions, the concept of continuity and complex differentiation.
So in no particular order, below are some notes on mistakes I made and how I could've avoided them! There's a lot to reflect on here...
Read questions carefully. One of the first very simple questions read "express  in polar form and determine all fourth roots". I did the second bit, but not the first.
in polar form and determine all fourth roots". I did the second bit, but not the first.
I feel this is a bit "Complex Numbers 101", but the square root sign is defined as the principal square root (of a complex number), i.e. there's no need to calculate the second root.
If you're using the triangle inequality, state it specifically.
Again, this is fairly "Complex Numbers 101", but the polar form of a complex number isn't just a cosine function as the real part, and a sine function as the imaginary part. The arguments to both functions must be identical to qualify as "polar form". ie, you should be able to write the complex number as an exponential form.
Top tip: Be mindful about using identities. In complex analysis there are loads of them and they help a great deal.
When working out the inverse of a complex function, it's important to use your common sense. Part of one inverse I'd calculated had a square root in it. Just by looking at that, you know it could never produce a unique answer (it isn't a one-to-one function).
For another, I had to find the inverse of 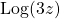 and the domain of that inverse. I got this spectacularly wrong. I'd written: given
and the domain of that inverse. I got this spectacularly wrong. I'd written: given 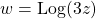 , hence
, hence 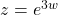 .
.
Trick here was to exponentiate each side, leading to 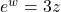 . But the domain of the inverse isn't affected by the "3" above, the image set of the original function is still
. But the domain of the inverse isn't affected by the "3" above, the image set of the original function is still 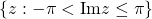 .
.
Some complex functions are very very different to their real equivalents. Case in point: 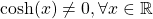 , but
, but 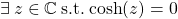 . Which leads to the next note:
. Which leads to the next note:
If 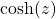 is the divisor in a complex quotient, you need to show that it's only 0 for values outside of the given range of the equation (eg
is the divisor in a complex quotient, you need to show that it's only 0 for values outside of the given range of the equation (eg  ).
).
For one question, I had to prove that 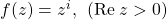 was continuous. I thought this was easy.
was continuous. I thought this was easy.
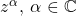 is a basic continuous function on
is a basic continuous function on 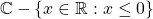 . So if you let
. So if you let 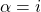 , then
, then 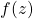 is continuous, right?
is continuous, right?
Not quite. I had entirely forgotten to state that the given set 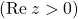 is a subset of the set I gave:
is a subset of the set I gave: 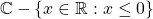 .
.
The answer can appear obvious sometimes, but you have to keep your answer rigorous, otherwise you risk losing half marks or whole marks here and there.
Note:
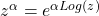
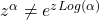
🙁
For one question I had to prove whether a set was a region or not. For reference, a region is a non-empty, connected, open subset of 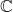 . In the usual manner, if you can prove that any of those three properties don't hold then you've managed to prove that your set isn't a region. Easy.
. In the usual manner, if you can prove that any of those three properties don't hold then you've managed to prove that your set isn't a region. Easy.
I realised I could prove a set was closed, and hence not a region. Turns out this was incorrect. A set being "closed" and a set being "not open" hold two completely different definitions, and are seen as different things. I was meant to show it was "not open" as opposed to showing it was "closed".
In other words, mathematically:
Closed is not the same as not-open.
Closed is not the opposite of open.
Not-open is the opposite of open.
Again, here I needed to provide a proof based on the properties of various objects. Given a set that was compact (closed and bounded), I needed to prove that a function 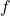 was bounded on that set.
was bounded on that set.
The Boundedness Theorem states that if a function is continuous on a compact set, then that function is bounded on that set.
The function was: 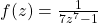
I proved that the given function was continuous on it's domain, but I'd failed to prove it was continuous on the set. Here, I needed to show where the function was undefined, THEN show that those points at which it was undefined all lay outside of the set. So there was quite a lot of work I missed out from this answer.
My simultaneous requirement for the Cauchy-Riemann theorem, AND the Cauchy-Riemann Converse theorem within a proof ended up not flowing very well logically. Once again, I'd jumped ahead with my logic. As soon as I had seen something obvious, I felt the urge to state it immediately.
The Cauchy-Riemann theorem proves that a function is not differentiable at certain points. The Converse theorem then proves that a function IS differentiable on certain points. After using the Cauchy-Riemann theorem, it was extremely obvious where the function was differentiable, so I stated it. Then, as a matter of course, plodded through the Converse theorem to prove it. Complete lack of discipline! 🙂