Still reading though my book in Analysis, I've come across a section on proving inequalities. I'm glad to say that all of this made sense... until I reached a sub-section on proving an inequality by mathematical induction.
As I've written previously, I find that proofs are notoriously unintuitive. In the past however, I have been particularly puzzled by the logical steps involved in proving an inequality by mathematical induction.
To explain my difficulties, let's have a look at the example provided in the book:
Prove that 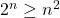 , for
, for 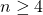 .
.
If we're proving this by mathematical induction, we generally follow these steps:
- Let
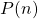 be the statement
be the statement 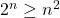 .
.
- Show that
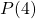 is true.
is true.
- Assume that
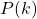 is also true for
is also true for 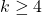 .
.
- Show that
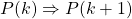 . Or rather, show that if
. Or rather, show that if 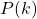 is true, then
is true, then 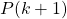 is also true.
is also true.
Step 4 is the key step here in the proof as it shows that if any number is true, and the next number is also true, then you can apply this rule forever, and your original statement must be true for all numbers!
Anyway, lets jump to step 2. Show that 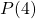 is true. Well if
is true. Well if 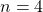 , then
, then 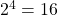 and
and 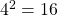 . So
. So 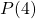 is true! Easy.
is true! Easy.
Let's look at step 3. Let's ASSUME that 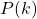 is true for some
is true for some 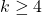 .
.
Now, this is the part that caught me by surprise... At this step, the text in the book reads as follows:
"So, we are assuming that 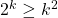 . Multiplying this inequality by 2 we get:
. Multiplying this inequality by 2 we get:
![Rendered by QuickLaTeX.com \[2^{k+1} \geq 2k^2\]](http://adrianbell.me/wp-content/ql-cache/quicklatex.com-66fc3b1a292c747cd77f128b74cc8359_l3.png)
,
so it is therefore sufficient to prove that 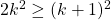 ."
."
Wait, what? How is it that all of a sudden, all we need to prove is that 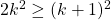 ? This isn't explained explicitly in the text so I had to close the book and do a bit more thinking.
? This isn't explained explicitly in the text so I had to close the book and do a bit more thinking.
First thing I had to realise here is that the "Step 4" I've listed above requires a bit more detail... What you're actually trying to do is show that you can progress naturally from 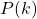 to
to 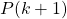 . ie: We should be able to show that we can progress naturally from:
. ie: We should be able to show that we can progress naturally from:
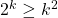
to:
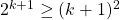 .
.
Now, if we multiply 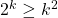 by 2, as mentioned in the text, we do arrive at:
by 2, as mentioned in the text, we do arrive at:

This is good, as we've managed to get the 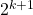 we were looking for on the left-hand side of the inequality. But the right-hand side looks nothing like the right-hand side of
we were looking for on the left-hand side of the inequality. But the right-hand side looks nothing like the right-hand side of 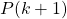 ie:
ie: 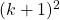 .
.
Here's the key though... It doesn't matter they they're not the same. We only need to see how 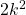 and
and 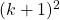 relate to each other. Look back at Step 3. Part of this assumption is that
relate to each other. Look back at Step 3. Part of this assumption is that 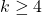 . Just as a test, let's try
. Just as a test, let's try 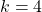 :
:
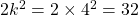
and
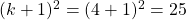
Well this is interesting. It's looking as if 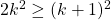 . This is exactly what was written in the text!
. This is exactly what was written in the text!
But to really ram it home, what we really have now is the following:
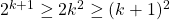
So.... this show us that IF we can prove that last bit 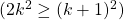 is true for all
is true for all 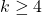 , and not just
, and not just 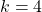 we have managed to prove that we can get from
we have managed to prove that we can get from 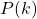 to
to 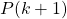 !!! This is exactly why the text in the book said "so it is therefore sufficient to prove that
!!! This is exactly why the text in the book said "so it is therefore sufficient to prove that 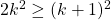 ."
."
I'm sure in future I'll jump on this immediately and say "oh yes, of course that's all we need to do now", but working through the derivation of why it was sufficient was extremely useful. Long-winded... but useful.
Ah, the learning process...