Pure Maths

Chapter 14 of 24 - Metric Spaces and Continuity 1

Again, this chapter was fairly merciful. First section was a natural progression from the last chapter, namely continuity of functions from \mathbb{R}^n to \mathbb{R}^m and a return to the all important triangle inequality from my complex analysis module last year.

Next section was great as it introduced a new mathematical object: the metric. Always fun, learning about something new like this. Though something that really tripped me up (that I feel I'm still struggling with now) is the geometry of metric spaces. There are sets defined around points in spaces called "balls", be it open or closed. I seem to have a big problem with defining what are inside and outside of these circular (in 2D) sets based on their defined radii. Sounds simple, but it seems it's not very intuitive. Not being able to define what's in your set is bad, so I need to do some further reading on this.

Next up was sequences in metric spaces, followed by the definition of continuity in metric spaces.

Pure Maths

Chapter 12 of 24 - Fermat's Last Theorem and Unique Factorisation

Finally at the half-way mark. This chapter took a long time to get through and the assignment was especially challenging. Again, I think I'll have a lot to write about once that is marked and returned.

The sections of chapter 12 were Fermat's Last Theorem and Diophantine equations, Integral Domains, Euclidean Domains, and Unique Factorisation Domains. There are subtle differences between all these different types of domains, even though the description of each one might very well just look like a construction of a polynomial.

For example, in integral domains, a prime and an irreducible are different things, but in Euclidean domains and UFDs, they're the same thing.

Also, one thing to note that I realised isn't in my handbook... norms can be constructed for polynomial domains. The norm is just the polynomial's degree. But this can only be done if the domain is a field.

Right, wow. What a journey. On to the next book. "Metric Spaces 1".

Pure Maths

Chapter 11 of 24 - Rings and Polynomials

New mathematical objects! Introduction to rings. Introduction to fields. Introduction to polynomial rings over fields. An interesting return to long division (!) with polynomial division, and some great examples of shortcuts for factorising polynomials and finding roots. Can't help but feel we should have been taught about these shortcuts earlier. Not only do they seem really valuable, they're also surprisingly interesting and can probably be taught without rings and fields as a prerequisite.

Group Theory, Proofs, Pure Maths

Assignment Result - Groups

My second assignment on groups was marked and returned. As predicted, there's a lot to take away from this.

Basic Groups

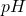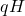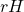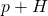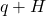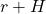At this level it seems it's not sufficient to use notation like pH, qH and rH to refer to subgroups. In my head, I know what the binary operator of these subgroups is but for the benefit of the reader the (better) convention is to be explicit with the binary operator: p+H, q+H, and r+H specifically.

Definition check: a cyclic group is just a group that contains a generator that generates the whole group. It doesn't have to "cycle" back to the beginning of the ordered set. eg, infinite sets can form a cyclic group under addition.

Mistakes in basic proofs. This one is a classic. With 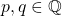p,q\in \mathbb{Q}, I had to prove 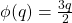\phi(q)=\frac{3q}{2} was onto. My answer:

\forall\: q\in\mathbb{Q},\: \exists\: p\in\mathbb{Q},\: \text{s.t.}\: \phi(p)=q,\: \therefore \phi

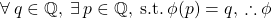
Which I was all smug about because it looks pretty. But this is just the definition of the function being onto and I'd neglected to state the actual 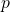p that always exists. Namely p=\frac{2q}{3}.

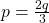Group Classification

Group decompositions can't be written as 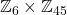\mathbb{Z}_{6} \times \mathbb{Z}_{45}. It needs to be written as 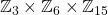\mathbb{Z}_{3} \times \mathbb{Z}_{6} \times \mathbb{Z}_{15}. 3 and 15 are not coprime, so cannot be combined.

Finite Groups

As a part of a group presentation, there are kind of identities like 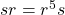sr=r^{5}s. However, for the most part in your answer, especially when you're talking directly about elements being in your group, they must always be in the form 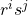r^{i}s^{j} (with r first).

In being asked to deduce an isomorphism, I heavy-handedly defined both groups (as they were small) and then also stated a function explicitly that would define the isomorphism. Apparently it's just enough to state that both groups were of order 2. Therefore they're isomorphic.

I need to become a lot more familiar with the concept of centres of a group. To show that a subgroup is the centre of its parent group, I needed to show that the subgroups elements were centres of the subgroup. I was was just trying to wing it, and although I essentially got the answer right, I showed I had a complete misunderstanding of centres.

Pure Maths

Chapter 10 of 24 - Quadratic Reciprocity

Fun chapter. Squares are very important, turns out. Chapter was about methods of solving quadratic formulas modulo some prime.

Covered Euler's Criterion for quadratic residues, The Legendre symbol, Gauss's Lemma, and then the law of quadratic reciprocity.

I'll be looking at rings next. I've been waiting to investigate these things for a while...

Pure Maths

Chapter 9 of 24 - Multiplicative Functions

Multiplication! That sounds nice and simple doesn't it! Unfortunately, that's not what that title means.

Any number can be broken down into its prime decomposition (15=3\times 5). A multiplicative function is where a function of a number is equal to the function of each prime in the prime decomposition of that number all multiplied together. So if n=p_1\times p_2, where p is a prime in the prime decomposition and if f(n) = f(p_{1}\times p_{2}) = f(p_{1})\times f(p_{2}), then the function f is a multiplicative function.

Next section went into detail about perfect numbers. A perfect number is equal to the sum of its positive factors excluding itself. Best example here is the perfect number 6=1+2+3.

The rest of the chapter was introducing Euler's \phi-function (also multiplicative), and using this new function, the introduction of primitive roots.

Group Theory, Pure Maths

Chapter 8 of 24 - The Sylow Theorems

Yet another confusing chapter that I couldn't spend enough time in. Overall, the Sylow Theorems just relate to subgroups of prime, and prime-power, order. Very generally, you can use the Sylow Theorems themselves to determine isomorphism and whether or not a group is a direct product of other cyclic groups.

That was the last of group theory! I'm about to submit my group theory assignment, and I can tell I'll have a lot to write about once that is returned. Next up, is the third book of the set, "Numbers and Rings".

Group Theory, Pure Maths

Chapter 7 of 24 - Finite Groups

I must admit, this one went by in a blur. First section was on describing groups, and introduced the idea of a group presentation. Second section was "conjugates, centralisers and centres", presenting some new concepts, followed by "groups of small order" which described how to work out what smaller groups were isomorphic to. The whole chapter ended with "finite p-groups" which discussed groups that were direct products of other groups of prime power order. This leads neatly to the next section which seems to be almost entirely be talking about groups of prime power order.

The learning curve is real.

Pure Maths

Assignment Result

One of the whole points of me starting this site was to write about the things I got wrong. Making mistakes is how you learn, right? My first assignment on number theory has been returned to me and it turns out I received 100% for it. Which is good. But it's also frustrating, because I don't feel that assignment reflected the difficulty of the material. Worrisome. Well this was assignment 1, I'm still at the beginning. Plenty of time to screw up yet.