Way way off the beaten path here, but this is the best example of usage of the pumping lemma I've seen. Just need somewhere to put it...
The below is taken from
here.
Theorem:
Let
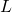
be a regular language, and
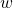
be a string. Then there exists a constant

s.t.
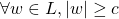
.
We can break
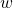
into three strings,
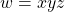
, s.t.:
Method to prove that a language 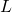 is not regular:
is not regular:
- At first, we have to assume that
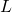 is regular.
is regular.
- So, the pumping lemma should hold for
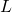 .
.
- Use the pumping lemma to obtain a contradiction:
- Select
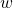 s.t.
s.t. 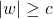 .
.
- Select
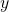 s.t.
s.t. 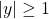 .
.
- Select
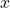 s.t.
s.t. 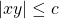
- Assign the remaining string to
 .
.
- Select
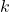 s.t. the resulting string is not in
s.t. the resulting string is not in 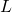 .
.
Problem:
Prove that
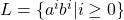
is not regular.
Solution:
- At first, we assume that
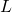 is regular and
is regular and 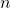 is the number of states.
is the number of states.
- Let
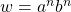 . Thus
. Thus 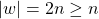 .
.
- By the pumping lemma, let
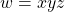 , where
, where 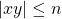 .
.
- Let
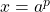 ,
, 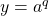 , and
, and 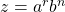 , where
, where 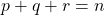 ,
, 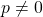 ,
, 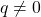 ,
, 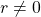 . Thusly
. Thusly 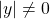 .
.
- Let
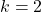 . Then
. Then 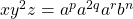 .
.
- Number of
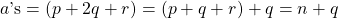 .
.
- Hence,
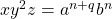 . Since
. Since 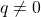 ,
, 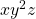 is not of the form
is not of the form 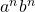 !!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!
- Thus,
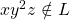 . Hence
. Hence 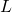 is not regular.
is not regular.
…is learning mathematics.
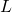 is regular.
is regular.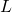 .
.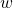 s.t.
s.t. 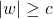 .
.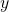 s.t.
s.t. 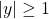 .
.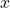 s.t.
s.t. 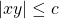
 .
.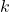 s.t. the resulting string is not in
s.t. the resulting string is not in 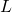 .
.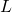 is regular and
is regular and 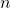 is the number of states.
is the number of states.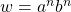 . Thus
. Thus 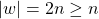 .
.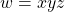 , where
, where 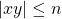 .
.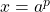 ,
, 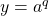 , and
, and 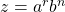 , where
, where 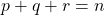 ,
, 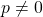 ,
, 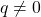 ,
, 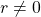 . Thusly
. Thusly 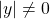 .
.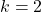 . Then
. Then 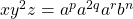 .
.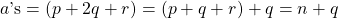 .
.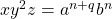 . Since
. Since 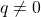 ,
, 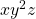 is not of the form
is not of the form 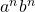 !!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!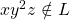 . Hence
. Hence 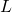 is not regular.
is not regular.