My second assignment has been marked! Very happy with these results. Though as usual, my tutor has been great and filled my paper with suggestions on how to improve further.

The identity axiom for a group: Often it's really obvious to see that an operation is commutative. Really easy. So easy in fact, that it's often just as easy not to mention that it's commutative. In doing so, you kind of miss out half the answer. Always check! If it works one way, always prove it works the other too!

Another obvious thing that's easy to miss out... mentioning that your result does actually lie within the required working set. ie: if you're working in the 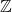universe, you need to explicitly say that your result is also in .

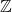All transformations are relative! I sped through these questions without thinking... silly really. I slipped up here, and never mentioned the point around which something was rotated, or the point around which a reflection line was rotated.

Students apparently screw this up a lot... me included it seems... but answers should be in their correct forms. I was so used to writing Cayley/Group tables as answers, I neglected to realise that the question actually wanted the set which formed the group. Here, effort was spent where it didn't need to be.

Lastly, I need to get better at quickly being able to spot if a Cayley table is Abelian (commutative). This was a silly oversight on my part. Something that's a little less obvious is how to quickly find a group that is isomorphic to my initial (Abelian, in this case) group. I suppose this will come with time and familiarity!

Next up we've got linear algebra. This looks like a big section, so it's good that I'll have the Christmas holidays to break the back of it!