Category Archives: Maths

Calculus

Integration Revision - Integration By Substitution

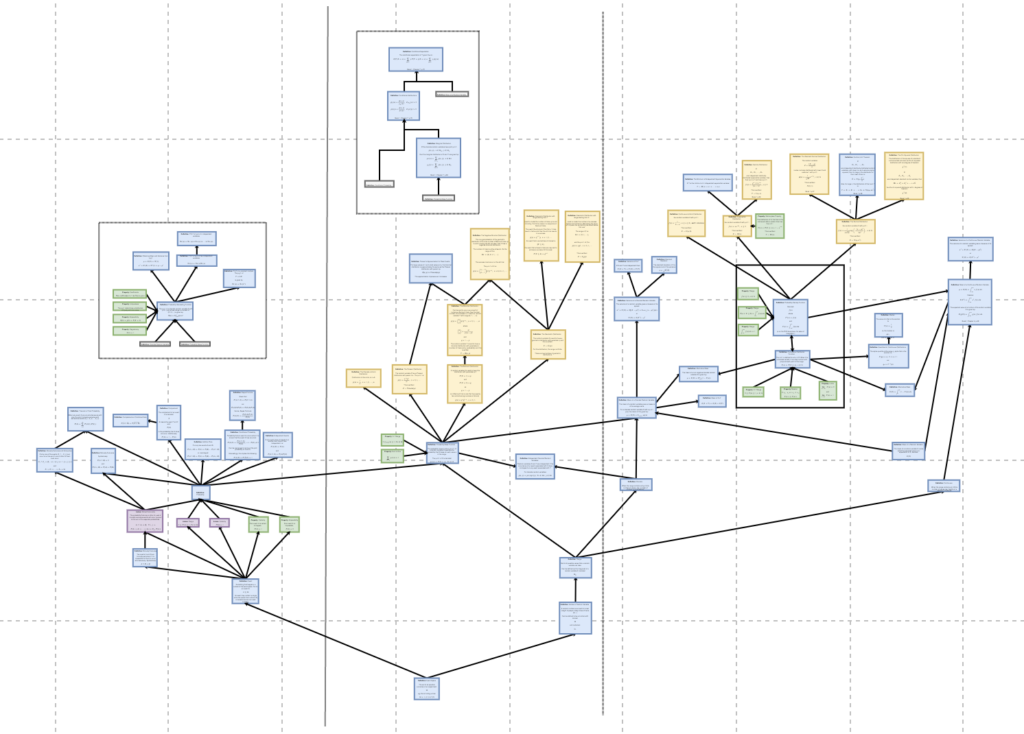
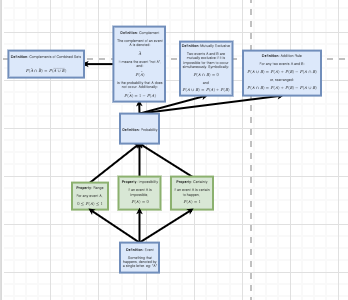
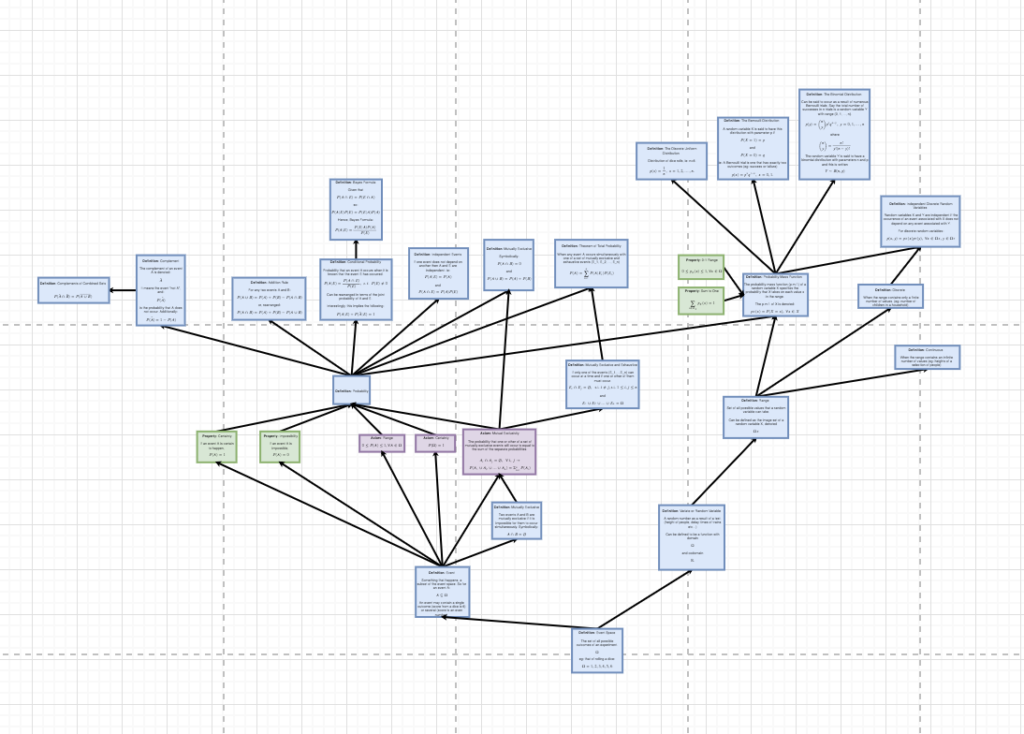
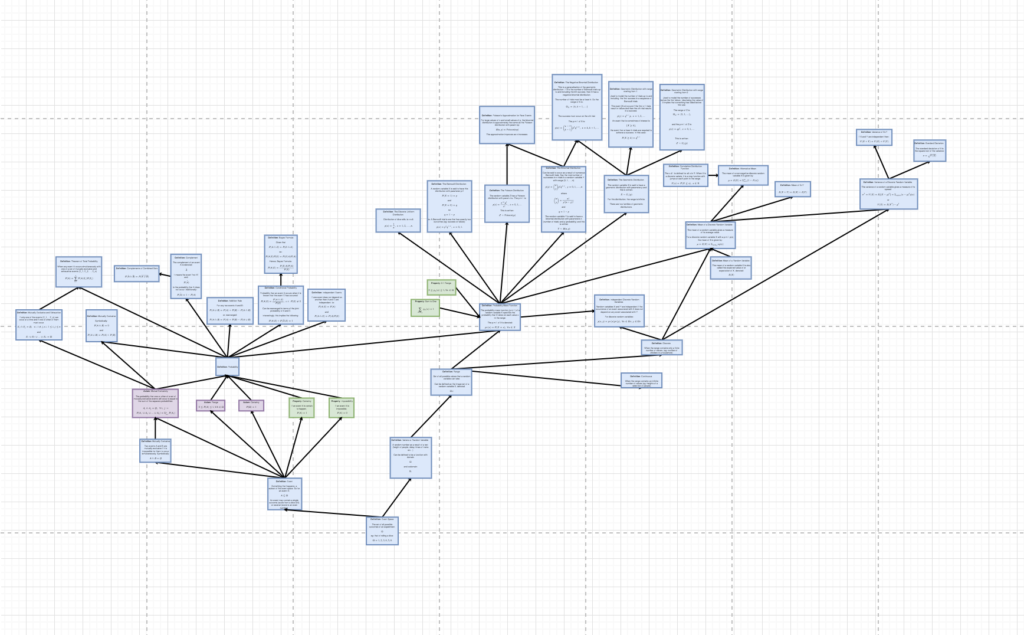
Now, looking at the other integral from Oct 13th...

\int^{x}_{0}4xe^{-2x^{2}}\:dx=1-e^{-2x^{2}}

In my opinion, this was scarier than the first, but looking at it again, what makes it scary is the various powers. e to the power of x to the power of 2 and such.

But why should this be scary? There's practically only one tool that one could use to solve this: the only tool that includes functions of functions, integration by substitution:

\int f(g(x))\:g^{\prime}(x)\:dx=\int f(u)\: du

In our case, the inner function:
g(x)=-2x^{2}=u
so:
g^{\prime}(x)=-4x

and the outer function:
f(x)=e^{x}

Plugging all these into our "integration by substitution" tool gives:

\int -4xe^{-2x^{2}}\:dx

But this is slightly different to the original integral due to that minus sign. Of course this is trivial to deal with as:

\int^{x}_{0}4xe^{-2x^{2}}\:dx=-\int^{x}_{0} -4xe^{-2x^{2}}\:dx

Great! So now we have the structure we require to apply integration by substitution! We can substitute all of that with f(u), and all the scary bits go away. So:

\int^{x}_{0}4xe^{-2x^{2}}\:dx

=-\int^{x}_{0} -4xe^{-2x^{2}}\:dx

=-\int^{u}_{0} e^{u}\:du

=-[ e^{u}]^{u}_{0}

=-(e^{u}-1)

=1-e^{u}

Then substituting u (=g(x)) back in:

=1-e^{-2x^{2}}

Calculus

Integration Revision - Integration By Parts, Twice

So looking at the first one from a few days ago (Oct 13th):

\int^{\infty}_{0}x^{2}\:\lambda\: e^{-\lambda x}\:dx=\frac{2}{\lambda^{2}}

I was totally lost with this. But running through some old tricks made this seem a lot more approachable. First off, moving the constant out brings a bit more clarity to the integrand,

\int^{\infty}_{0}x^{2}\lambda e^{-\lambda x}\:dx=\lambda\int^{\infty}_{0}x^{2} e^{-\lambda x}\:dx

But given the x^{2} and the exponential, we'll also probably need to use integration by parts:

\int^{b}_{a} f(x)g^{\prime}(x)dx=[f(x)g(x)]^{b}_{a}-\int^{b}_{a} f^{\prime}(x)g(x)dx

So, as above, letting:
f(x)=x^{2}
g^{\prime}(x)=e^{-\lambda x},

we have:
f^{\prime}(x)=2x
g(x)=-\frac{1}{\lambda}e^{-\lambda x}

Then plugging f, f^{\prime}, g and g^{\prime} into our lovely integration by parts tool above gives:

\lambda\int^{\infty}_{0}x^{2}\: e^{-\lambda x}\:dx

=\lambda\left(\left[-x^{2}\: \frac{1}{\lambda}\:e^{-\lambda x}\right]^{\infty}_{0}-\int^{\infty}_{0}-2x\:\frac{1}{\lambda}\: e^{-\lambda x}\:dx\right)

=\lambda\left(0-0+2\frac{1}{\lambda}\int^{\infty}_{0}x\: e^{-\lambda x}\:dx\right)

=2\int^{\infty}_{0}x\: e^{-\lambda x}\:dx

Which looks very familiar with what we've started with, except x^{2} is now just x! If we can reduce x by another power, we'll end up with just 1 which will surely give us a much easier integral to solve.

So applying integration by parts again, but letting:
f(x)=x
g^{\prime}(x)=e^{-\lambda x},

we have:
f^{\prime}(x)=1
g(x)=-\frac{1}{\lambda}e^{-\lambda x}

Then:

2\int^{\infty}_{0}x\: e^{-\lambda x}\:dx

=2\left(\left[-x\: \frac{1}{\lambda}\:e^{-\lambda x}\right]^{\infty}_{0}-\int^{\infty}_{0}-\frac{1}{\lambda}\: e^{-\lambda x}\:dx\right)

=2\left(0-0+\frac{1}{\lambda}\int^{\infty}_{0} e^{-\lambda x}\:dx\right)

=\frac{2}{\lambda}\int^{\infty}_{0} e^{-\lambda x}\:dx

=\frac{2}{\lambda}\left[-\frac{1}{\lambda}\:e^{-\lambda x}\right]^{\infty}_{0}

=\frac{2}{\lambda}\left(0-\left(-\frac{1}{\lambda}\right)\right)

=\frac{2}{\lambda}\:\frac{1}{\lambda}

=\frac{2}{\lambda^{2}}

Statistics

End of Book 1 - Review of Understanding

A quick look at the mind map I produced for the whole of Book 1, very much a foundation for the rest of the materials on the module.

The complexity has increased necessarily, but I'd like to think the clutter has been reduced to a minimum. I was rearranging nodes as I was adding them in the hope of reducing clutter. You'll notice there are two white floating boxes not connected to anything externally. This was just to avoid clutter.

Some things to note about it that help me refer back to it:

It's split roughly into thirds, vertically. Each third is more or less a sub topic. More like themes, perhaps. Far left is foundational principles. Middle relates to basics of distributions. Far right is concepts surrounding the C.D.F. and P.D.F. (the definitions of which are in the white box in the middle of the far-right section).

Colouring helps a lot when needing to refer back to it, I found. Axioms are pink, properties are green, and definitions are blue. I found that in referring back to it, I needed some kind of differentiation between the definition of a certain distribution, and a normal definition. So all the yellow nodes you see are definitions of distributions.

In summary, to assist my understanding, I now have a graph that leads me from the most basics concept (like what an "event" is), to the definition of the standard normal distribution. I'll be referring back to this as I go!

Calculus, Statistics

Integration Revision

Putting these in a safe place for later. Found these to be a really good revision questions for integration.

\int^{\infty}_{0}x^{2}\lambda e^{-\lambda x}\:dx=\frac{2}{\lambda^{2}}

and

\int^{x}_{0}4xe^{-2x^{2}}\:dx=1-e^{-2x^{2}}

For context, the first one formed part of a question that required me to find the variance of a random variable, and the second one involved having to find the c.d.f. from a p.d.f.

(for my own reference, this was Book 1, Activity 5.2, p. 54 and Activity 6.1, p.62)

General, Maths, Statistics

Current Application of Mind Maps

I've finally completed the second section of the first book, and it's served as a good revision/introduction session. I'm glad I went to the trouble of creating a mind map for the main concepts that were covered. Here's how my mind map grew as I added to it:

\/

\/

I've used this new mind map to refer back to several times during the exercises I've been set, and even the first assignment question. Admittedly it takes longer to get through all the learning material, as you have to take time out to contribute to the mind map as you go. Though I would say the time spent is worth it.

I also felt that this last image was the maximum size a mind map could take without becoming too cluttered. For the next section of the book, I'll be starting a brand new mind map. I'll try to keep going with this method for as long as I can, but it seems it's very useful.

Statistics

Module Number 7!

Summer is over!

Autumn is here!

That can only mean the new academic year is about to begin! (and the first module of the third and final stage of my degree!)

Up next? Applications of Probability (M343)!

I'm excited about starting this. When I started on this degree, I saw that there weren't many options for stats modules in the final stage unless you were specifically aiming toward a BSc in Statistics. I've read a number of articles discussing how there isn't enough stats in education at the moment and I'm inclined to agree. I'm hoping this will round my skills out nicely.

For all the info on this next module, check out the official page here.

The module website for students is due to open tomorrow, so I'll get access to all my materials and be allocated a tutor. What makes this module a little bit different is that it's a single credit module. The last two modules I've had (mathematical modelling and pure mathematics) were double-credit. So I'm wondering whether the workload will feel really light or not. I'm hoping it will be lighter, so I can contribute on here more frequently than for the last two!

General, Maths

The London Mathematical Society

In November '18, I decided to join the London Mathematical Society (LMS). Last month I attended a meeting there in Russell Square in Central London which involved a couple of lectures and a "swearing in" of new members.

As a part of the swearing in, new members have the opportunity to sign the LMS Member's Book. Interesting thing about this is it dates back to 1865(!). So after signing it, I flicked back the pages to find the signatures of both Arthur Cayley on June 19th 1865:

and James Clerk Maxwell on April 25th 1867:

Maths, Mechanics

A Lack of Updates

Study has been so busy this year, I've failed in keeping an up-to-date account of how it's been going. Here's a very quick run-though:

Assignment 2:

  • First and second-order differential equations.
  • Vector algebra and statics. (There are two blocks connected with taut string on a ramp and nothing is moving, what are the forces?)
  • Dynamics. (A block is sliding down a ramp with a certain friction, what are the forces?)

Assignment 3:

  • Matrices and determinants.
  • Eigenvalues and eigenvectors.
  • Systems of linear differential equations. (solving simultaneous differential equations).
  • Functions of several variables. (

        \[f(x,y)\]

    and

        \[f^{\prime}(x,y)\]

    instead of

        \[f(x)\]

    and

        \[f^{\prime}(x)\]

    ).

Assignment 4:

  • Mathematical modelling. (Introduction to writing a mathematical modelling paper).
  • Oscillations and energy. (Forces in a spring system, and potential energy).
  • Forcing, damping an resonance. (Forces in a system of springs and dampers).
  • Normal modes. (Oscillations of particles in a spring system).

Assignment 5:

  • Systems of differential equations. (Equilibrium points of two differential equations and use of the Jacobian matrix).
  • Fourier series.
  • Partial differential equations.

Assignment 6:

  • Vector calculus. (Scalar fields and gradients).
  • Further vector calculus. (Conservative vector fields, curl, and divergence).
  • Multiple integrals. (Area and volume integrals).

Assignment 7:

  • Writing a 3000-word mathematical modelling paper.

All the above are now complete, and I'm currently working through the last few units. Namely:

  • Systems of particles.
  • Circular motion.
  • Rotating bodies and angular momentum.

There's a requirement for me to submit one assignment per month, from October to May. These double-credit modules are hectic...

Out of all of the above, Assignment 7 had to be the most nerve-racking. Most assignments normally read like exam papers, though for Assignment 7 I had to write a report. So not only had I never written a report like this on this course before, I'd never written a report like this ever! Results are due in a couple of weeks, so based on the outcome I'll be keen to break down where I went wrong.

Favourite bits from the above have to include my first ever hand-calculation of a Fourier series in Assignment 5, and a question where I had to prove a result of Archimedes (287-212 BCE) regarding relative volumes, using modern calculus in Assignment 6. I'd also always wanted to know more about the construction of a Jacobian, so Assignment 5 was good for applying my new knowledge.

Automata Theory, Proofs, Pure Maths

Pumping Lemma

Way way off the beaten path here, but this is the best example of usage of the pumping lemma I've seen. Just need somewhere to put it... The below is taken from here. Theorem: Let L be a regular language, and w be a string. Then there exists a constant c s.t. \forall w \in L, |w| \geq c. We can break w into three strings, w=xyz, s.t.:
  • |y| > 0
  • |xy| \leq c
  • \forall k \geq 0, xy^{k}z \in L
Method to prove that a language L is not regular:
  • At first, we have to assume that L is regular.
  • So, the pumping lemma should hold for L.
  • Use the pumping lemma to obtain a contradiction:
  • Select w s.t. |w| \geq c.
  • Select y s.t. |y| \geq 1.
  • Select x s.t. |xy| \leq c
  • Assign the remaining string to z.
  • Select k s.t. the resulting string is not in L.
  Problem: Prove that L=\{a^{i}b^{i} | i \geq 0\} is not regular. Solution:
  • At first, we assume that L is regular and n is the number of states.
  • Let w=a^{n}b^{n}. Thus |w|=2n\geq n.
  • By the pumping lemma, let w=xyz, where |xy| \leq n.
  • Let x=a^{p}, y=a^{q}, and z=a^{r}b^{n}, where p+q+r=n, p \neq 0, q \neq 0, r \neq 0. Thusly |y| \neq 0.
  • Let k=2. Then xy^{2}z=a^{p}a^{2q}a^{r}b^{n}.
  • Number of a\text{'s}=(p+2q+r) = (p+q+r)+q=n+q.
  • Hence, xy^{2}z=a^{n+q}b^{n}. Since q\neq 0, xy^{2}z is not of the form a^{n}b^{n}!!!!!!!!!!!!!!!
  • Thus, xy^{2}z \notin L. Hence L is not regular.