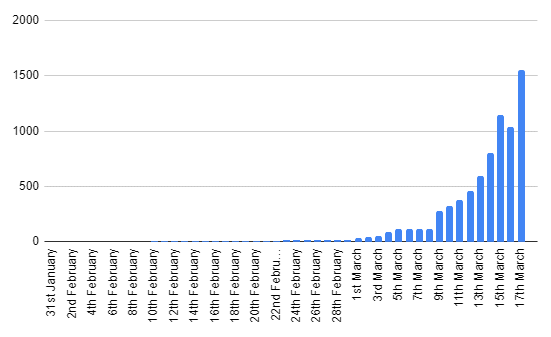
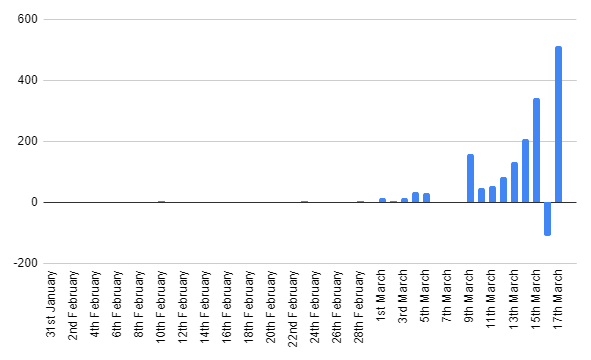
So I've finally completed all my assignments! I've just had the very last one returned to me and again, although I did well, there are very obviously some areas for improvement:
Models for Populations
Very small thing here, but when asked to describe the shape of the age-specific death rate, it's important to describe it in terms of the rate (of change).
Genetics
Wow. My weakest area by a long way here... It'd be wise for me to avoid any exam questions on genetics... But for the moment, let's examine what I did wrong to try and understand the assignment questions better at least. (It's mainly an issue with conditional probabilities).
Proportions
When calculating the probabilities of genotype combinations of parents, if you're given the genotype of one parent you don't need to use it in the calculation! eg: Despite the proportion of a genotype in a population being 0.2, if you're given the genotype of one parent, then the chance of them being that genotype is 1.0, not 0.2! Making a mistake like this obviously has a knock-on effect on working out probabilities for the children's genetics, insofar as the probabilities of the children will be incorrect too.
But I compounded my issue with the children. It took me a while to review the next bit to work out where I went wrong, but here we go...
When working out the parent-child genetics, you start by working out two sets of probabilities:
- The probability of the parents being certain combinations of genotype (easy in this specific case, as the probability of one parent is 1.0). The probability of the parent of unknown genotype follows from the Hardy-Weinberg law. We'll call the probability of all the mating types
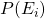 .
.
- The offspring probabilities, which follow from Mendel's first law. Though we'll talk about them in terms of phenotype, so
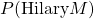 means the probability of Hilary being of phenotype M.
means the probability of Hilary being of phenotype M.
So the next question asked just that: What is the probability of Hilary being phenotype M (which was just one genotype "MM").
This question I managed to get correct based on my initial incorrect probabilities of the parents, but it's important to explain it for the next question. So it turns out that:
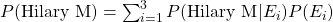
So you multiply each offspring probability, (the probability of Hilary being phenotype M given the mating type) with the associated mating type probability. And you sum them across all mating types. Easy.
But the next question was:
Calculate the probability that sisters Hilary and Jane both have phenotype M. This was the bit that I got completely wrong that took me a while to review. I ended up squaring the result I got from the last question. Very not correct. 🙁 From the above, we know we start with:
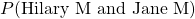
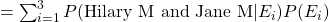
and it turns out:
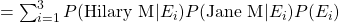
Which suddenly makes it all very very clear. I suppose this goes to show that when you come across something convoluted, it's worth taking extra time out to run through it in depth and make detailed notes on it. Doing so here would've paid off. I think the problem I have with genetics questions is that there are quite a number of ways in which these questions can be phrased.
Writing Conditional Probabilities
Well this went really wrong. This is probably my weakest area, and is related to the above slip-ups in the questions with Hilary and Jane.
"Show the that proportion of male offspring for the second mating that you should expect to have plain wings (gene contains dominant allele A) is 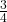 ."
."
Here, I wrote the definition incorrectly, but calculated the correct result. Kind of double-bad. 🙁 Here, I wrote:
P(male A)
(which is the joint probability of a male having the allele A)
When I should have written:
P(A | male)
(the conditional probability of offspring having the allele A given that they're male.)
The Hardy-Weinberg Law
A lengthier title to this subsection would be: "When to calculate the proportions of subsequent generations of a certain type using Hardy-Weinberg, and when to use your own table of probabilities".
As above, the table of probabilities includes the probabilities of the parents of certain types mating, and the probabilities of the associated offspring genotypes.
The question:
"One male and one female are chosen at random from all the offspring of the mating, and are themselves mated. What is the proportion of female offspring of the second mating to have a dominant allele?"
In this case, there were two genotypes which had a dominant allele, AA and Aa. But how do I parse this question? This question is asking about grandchildren of the initial parents! It's also asking about "proportion" which hints that I should be using Hardy-Weinberg proportions. Turns out not. It seems that you can only use the Hardy-Weinberg law when you're given the proportion of three genotypes of a starting generation.
So what are we left with?
P(AA | female) AND P(Aa | female)
Which in this case is equivalent to:
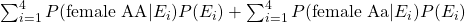
Notice how this differs from the sum in the last section (the Hilary and Jane example), because there's no assumption made about them both having the same father.
Last related one here that tripped me up was:
"What is the proportion of dominant-alleled females in this second mating would you expect to be AA?"
Again, I used the Hardy-Weinberg law to calculate this, when I should've been using conditional probability.
So it seems I needed to go through the process of parsing the question, and translating it into stats language: "What's the probability of offspring being genotype AA given that they're a female with a dominant allele?". The probability we require here is:
P(AA | dominant allele female)
Using the standard, straight-forward rule for conditional probability I learned in my first section back in September, this is equivalent to:
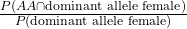
What's the numerator here? The probability of being AA and a dominant-allele female? Well yeah, AA is dominant, we know that. So this is just the probability of being AA and female:
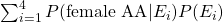
It's just one part of the previous question.
Then what's the denominator? The probability of being (proportion of) a dominant-allele female generally? So AA female and Aa female? Well that was the actual answer to the last question!
So that's it. There's a lot of parsing that needs to be done generally:
Have I been given proportions? Use Hardy-Weinberg.
No proportions? Use a table of parents and offspring probabilites.
What am I given, what don't I have to calculate?
What are they asking me, is the probability conditional?
If it's conditional, I can separate it out but then I need to parse what each of these new probabilities mean.
Armed with this little checklist, I may have done a bit better in my genetics questions!
General Stuff
Range
If your answer is an equation in terms of x, always state the range of possible values of x:
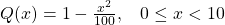
Variance
Annoying oversight here. When stating the variance of the lifetime of something was 42.92 months, I should've said it was 42.92 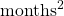 . Not often you think of months-squared, but here, it's relevant. Variance!
. Not often you think of months-squared, but here, it's relevant. Variance!
Log and Ln
Concentrate when typing one or the other into your calculator. There's a big difference, people... Thankfully I only slipped up once here.
And that's it! Now it's just revision time until my exam on the 8th of June. Of course, due to our new friend covid-19, I'll be taking my exam at home which will be a bit weird. Plenty to revise though, so I'll get started...
 of
of  .
.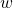 is a function of
is a function of  (to discover the condition under which
(to discover the condition under which 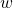 remains valid.
remains valid.![]() :
: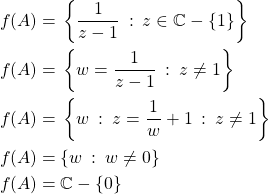
![]() ) of the domains of all component functions and that of the combined function. e.g:
) of the domains of all component functions and that of the combined function. e.g:![]()
![]()
![]()
![]() and
and ![]() with domains
with domains ![]() and
and ![]() respectively, the domain of
respectively, the domain of ![]() is:
is:![]()
![]()
![]()
![]()
![]()
![]()
![]()
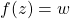 .
.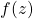 to find a unique
to find a unique  in the domain of
in the domain of 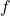 .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() gives a unique soluition in
gives a unique soluition in ![]() , hence
, hence ![]() has a unique inverse rule:
has a unique inverse rule:![]()