Last Assignment Submitted

April 25, 2017 Adrian Leave a comment

In just over a month and a week I've submitted two 20+ page assignments. I'm exhausted.

The last section on Real Analysis was incredibly challenging. I was so short on time I realised I would've have enough time to type up the assignment for it in LaTeX, so I re-wrote all my answers neatly on paper just like the old days. In fact, I was SO tight on time, even after all this, I almost didn't make the submission. Never been so close to missing a deadline.

But overall, that whole month was incredibly stressful. I'm not sure how to avoid that kind of stress in future other than making sure I'm way ahead of the deadlines for the whole academic year. -and that's incredibly hard to do for a double-credit module like this one if you're working full-time. Yeah, that was unpleasant.

Anyway. Luckily, after all that, I had booked two weeks off for Easter. This meant my final assignment wouldn't be so much of a rush. The final assignment consisted of questions on everything from the entire academic year. There was no new material to learn for it, hence the two week deadline. Though if I hadn't taken this holiday, I don't think I would have been able to find the time to complete this last assignment. There was still a very large amount of work to do.

However... today I have submitted this last assignment too. That's it. All seven assignments complete. Material learnt. Course done.

All that's left is six weeks of revision, which will include a revision weekend off at the Open University campus in Milton Keynes. A rare chance to sit amongst fellow maths students. Although it very much isn't a break, I'll be treating it like one as I get to escape from London for a couple of days.

In fact, on the Friday I drive up I'll be stopping off at Bletchley Park! Expect photos in a few weeks...

In the mean time, I'm going to make an attempt to relax a little in my final week of vacation before going back to work and starting my revision period. Let's see if I can get my mind refreshed before the final push...

Group Theory

The Last Group Theory Feedback

March 21, 2017 Adrian Leave a comment

My fifth assignment has been returned! And with it, the usual amount of feedback!

In this assignment, I failed to realise that a subgroup is normal if it is a union of conjugacy classes. So rather than form subgroups and state they were a union of conjugacy classes, I went through the process of proving each group was a sub group. Too long-winded, and frankly a waste of time. (for reference, this refers to Theorem 3.5 on properties of subgroups, p.74 in the handbook for M208).

There was another question where I had to show that a particular group had no subgroup of order 4. I took this rather literally, and found the only 4 possible combinations of elements that could be a subgroup of order 4, and then individually proved each one did not qualify either as a subgroup or as normal. Again, although I received full marks for this as it was correct, it was long-winded. It seems that all I needed to notice that a group of order 4 is either a typical cyclic group of order 4 ( 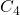$C_{4}$ ), or a Klein group ( 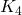$K_{4}$ ). A property of 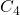$C_{4}$ is that it contains an element of order 4. But the question says the group has no subgroup of order 4! Therefore, my possible subgroups must be isomorphic to 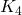$K_{4}$ . Property of 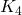$K_{4}$ : it contains three elements of order 2. This cuts the number of possibilities in half. Amazing how mindful you have to be of the properties of everything...

When having to write down subgroups of a matrix group I thought I'd written two different subgroups, but they were actually the same. One of the entries in one subgroup was 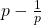$p-\frac{1}{p}$ , and the other was 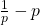$\frac{1}{p}-p$ . Now, these ARE both different. But they don't constitute as different general entries in my matrix, because they are both in 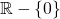$\mathbb{R}-\{0\}$ . The correct answer had the second matrix with an entry that read 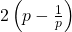$2\left(p-\frac{1}{p}\right)$ , which of course has a different domain: 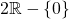$2\mathbb{R}-\{0\}$ , so it forms a different sub group. My brain had clearly just seen two different formulas and had gone "there we go, they're different!". Not so. Domains for subgroups must be checked!

This is incredibly easy to forget: When trying to prove something is not true, don't leave it at the generalised proof that it's not true. If it's not true, provide a specific counter-example. With numbers! Remember those? The things that you count with that aren't letters? Duh! Yes, so I know to be vigilant now...

I had some trouble explaining a mapping of complex numbers in English. This is problematic. I could've programmed it and shown you the mapping and in an instant you would've thought "ah yeah!". But with lengthy explanations about how we get to the point where the real part gets mapped to the inverse of the imaginary etc etc... things can get a bit muddled. It seems I need to resort to explaining things mathematically more often, using the facts I already have.

I need to do more reading on the Isomorphism Theorem (specifically with regard to the domain of the Image that the quotient group is isomorphic to). Wow, that was a bit wordy... Ultimately I need to be more mindful about domains of Images...

So that's it! Again, happy with my high mark, but lots to remain mindful of...

Analysis

Real Analysis Feedback

February 26, 2017 Adrian Leave a comment

As it turns out, that wasn't as bad as I thought it would be. Had some significant time constraints, and some of the concepts of continuity really threw me near the end but it wasn't a total nightmare.

Must admit though, there are still some areas which I feel I still need to "grok". (Hmm... never much liked that word... but replacing it with "understand intuitively" doesn't quite sound right either, but you know what I mean.) Concepts of continuity is one such area that I'll have to spend some extra time on in the revision stage (or maybe even just before my final Analysis section).

In summary, this was certainly the most challenging section yet. Having said that, I did manage to achieve a higher mark than I expected to get in my assignment. As usual, here are some areas in which I screwed up:

It seems intuitive to say that $0 + \infty + 0 = \infty$ , but this specific rule regarding the sum of these limits was never listed in the set that I can use, so I can't use it, hence I was marked down. I've always enjoyed working with a limited toolset, so this should come naturally after a bit of revision. The main problem is getting that full understanding of the mechanics of each rule so it can become intuitive. In fact, my answer for this particular question (as a consequence) was extremely drawn-out. The proper answer given by my tutor fits on less than half a page of A4. Hopefully more practise will let me see the quick, correct answer more quickly.

I stated Bernoulli's Inequality incorrectly. Absolutely no excuse for that. 🙁

When working out limits of formulas, always state the dominant term before reducing, and always put curly brackets around a sequence (otherwise, it's just a formula).

In some cases I was lazy and claimed that something like $\frac{3}{n+2}$ was a basic null sequence. Although it is quite obviously basic, and quite obviously a null sequence (it converges to 0 as n increases), it's not actually a basic null sequence. So even something as small as this, I need to deconstruct and prove.

Lastly, and this does bear repeating... I need a lot more practise with questions about continuity...

Next up, more group theory!

Analysis

Time Constraints

February 12, 2017 Adrian Leave a comment

I'm coming towards the end of my last section of my Analysis. I'm probably about half-way through the last book. After that, I have to answer the last question in my Analysis assignment, proof read the whole thing and submit it.

I have the whole of today, Monday, Tuesday and Wednesday before I need to submit this Analysis assignment. To make sure I can submit this assignment in time, and get ahead for my next section (Group Theory Part 2), I've taken the Monday, Tuesday and Wednesday as holiday days. That'll make a total of 5 days I've taken off work since the beginning of January just to make sure I'm where I want to be with my study.

There's a ebb and flow to where I am with my study compared to where I should be, and I won't truly understand how well I managed my time until this whole module is over in June, but I sure wasn't expecting I'd have to use holiday days to catch up on study.

One of the most frustrating things about feeling like you're behind is the nagging feeling like you don't have sufficient time to learn the materials sufficiently. This slight panic creeps in and you realise that more than anything else, you need to reach the end of the section (to be able to move on to the related assignment question). So you learn it JUST well enough to move on. Of ALL the sections for this to happen on, it had to happen with Analysis didn't it. The section I was most nervous about.

So in summary, because I've found myself short on time, I'm having to practically rush through the section on Analysis. No time for playing with concepts, no time to study the proofs in depth (or at all in some cases). Just time to get the general gist, and move on.

Something I will say is that I haven't found it necessary to keep a spider diagram of how core concepts relate to one another. Because of the structure of the learning materials I find it fairly easy to see the links and how one theory supports another proof and so on.

What has been a surprise while studying analysis is that there hasn't been a need to write any proofs in quite the same way as I was expecting. It turns out that (so far, at least) there isn't a need to have an in-depth understanding of logical notation or concepts. You need a basic understanding of the "if x, then y" structure, and the consequential converse "If not y, then not x", and so on, but not a great deal more. I'm not sure whether I'm grateful for this or not. Some of the concepts in Analysis require all my brain power, so I'm not sure the additional logical puzzles on top of that would help. Though on the other hand, having a decent foundation in logic feels quite important. I suppose, again, I'll have formed a more solid opinion on this by the end of the module.

Linear Algebra

Linear Algebra Feedback

February 5, 2017 Adrian Leave a comment

Received another good mark for this assignment, which I'm happy about as at the last minute I realised I'd messed one question up so re-did it. Though despite the high mark, I had a lot of great feedback from my tutor.

Overwhelmingly, he mentioned that I had to use more English to explain why I was solving a question in a certain way. This struck a chord with me as the more solutions I read, the less English there appears to be explaining the methods used, and ever since starting this Mathematics journey this is something I've had issue with. Some people find Mathematics hard to get into because of the certain barriers to entry, ie: the text won't fully explain what a variable is or (case in point) won't explain how to get from one step to the next. Often such a step is taken as "obvious", and I've always considered this as somewhat "elitist". With this assignment I've face-palmingly found myself falling into the same trap.

This is doubly interesting for me, as I actually do really enjoy going into lots of detail in explaining something I've worked on. So in future, I'll be mindful to explain more of my workings in plain English; or at least summarise them in plain English.

Linear Algebra

January 22, 2017 Adrian Leave a comment

Blimey. That was a journey... I've always wanted to know more about mathematics in dimensions higher than 3. Turns out I should be careful what I wish for!

Given my background and prior knowledge of 3d transformations, I thought I might find this section rather easy. Though shortly after starting it, I was forced to think about what would constitute an orthonormal basis in four dimensions. Needless to say, this is not only unintuitive, but also impossible to imagine (and as a colleague quite correctly pointed out, impossible to draw!). So instead of relying on intuition, you rely on basic generalised properties of manipulation of bases. After that, you can work in any dimension you want!

Interestingly, amongst all this talk of linear transforms and bases, there was not one mention of cross products. Everything was done without the need for them, which is an eye-opener given the liberal scattering of cross products in my own transformation code!

Perhaps one of the most interesting things I looked at was a description of a basis in four dimensions that you go on to prove is actually representable in three dimensions. Obviously, it's not always possible to do, but this representation of higher dimensions in lower ones was something else I'd been interested in for a while. The 4D window on dimensionality has begun to open!

This section was really fun. It's a shame there is only one section on it this time around. Next up... the dreaded Analysis...

Books, Pop Books

A Romance Of Many Dimensions

December 23, 2016 Adrian Leave a comment

I decided to buy Flatland: A Romance Of Many Dimensions by Edwin A. Abbott. Glad to say I got exactly what I wanted out of it: a light read!

It mostly takes the form of a light societal allegory, using aspects of multiple dimensions and a little bit of philosophy thrown in there for good measure too. Though I feel it didn't take itself too seriously and did make me smile on occasion. Something this book doesn't do is help you think in four dimensions and higher, though it does make you think a little more about the dimensions we can visualise in our heads!

Entertaining all the way though, it's a great, light read should you be requiring one!

…is learning mathematics.